题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)令![]() ,判断函数
,判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)令![]() ,
,![]() 的最大值为A,函数
的最大值为A,函数![]() 在区间
在区间![]() 上单调递增函数,求
上单调递增函数,求![]() 的取值范围;
的取值范围;
(3)令![]() ,将函数
,将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图像,对任意
的图像,对任意![]() ,求
,求![]() 在区间
在区间![]() 上零点个数的所有可能值.
上零点个数的所有可能值.
【答案】(1)非奇非偶函数,理由见解析;(2)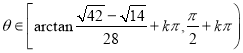 ;(3)见解析
;(3)见解析
【解析】
(1)特值法:ω=1时,写出f(x)、F(x),求出F(![]() )、F(
)、F(![]() ),结合函数奇偶性的定义可作出正确判断;
),结合函数奇偶性的定义可作出正确判断;
(2)当![]() 时,利用诱导公式、两角和的正弦公式展开及辅助角公式求得h(x),进而求得h(x)的最大值A,由题意可知:对称轴
时,利用诱导公式、两角和的正弦公式展开及辅助角公式求得h(x),进而求得h(x)的最大值A,由题意可知:对称轴![]() ,解得
,解得![]() ,即可求得θ的取值范围.
,即可求得θ的取值范围.
(3)根据图象平移变换求出g(x),令g(x)=0可得g(x)可能的零点,而[a,a+10π]恰含10个周期,分a是零点,a不是零点两种情况讨论,结合图象可得g(x)在[a,a+10π]上零点个数的所有可能值;
(1)当![]() 时,f(x)=2sinx,
时,f(x)=2sinx,
∴F(x)=f(x)+f(x![]() )=2sinx+2sin(x
)=2sinx+2sin(x![]() )=2(sinx+cosx),
)=2(sinx+cosx),
F(![]() )=2
)=2![]() ,F(
,F(![]() )=0,F(
)=0,F(![]() )≠F(
)≠F(![]() ),F(
),F(![]() )≠﹣F(
)≠﹣F(![]() ),
),
所以,F(x)既不是奇函数,也不是偶函数.
(2)当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
∵![]() ∴
∴![]()
由题意,![]() 在区间
在区间 上单调递减
上单调递减
∴抛物线对称轴![]() ,即
,即![]()
∴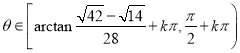
(3)f(x)=2sin2x,
将y=f(x)的图象向左平移![]() 个单位,再向上平移1个单位后得到y=2sin2(x
个单位,再向上平移1个单位后得到y=2sin2(x![]() )+1的图象,所以g(x)=2sin2(x
)+1的图象,所以g(x)=2sin2(x![]() )+1.
)+1.
令g(x)=0,得x=kπ![]() 或x=kπ
或x=kπ![]() (k∈z),
(k∈z),
因为[a,a+10π]恰含10个周期,所以,当a是零点时,在[a,a+10π]上零点个数21,
当a不是零点时,a+kπ(k∈z)也都不是零点,区间[a+kπ,a+(k+1)π]上恰有两个零点,故在[a,a+10π]上有20个零点.
综上,y=g(x)在[a,a+10π]上零点个数的所有可能值为21或20.
