题目内容
【题目】已知函数![]()
(1)判断函数![]() 的奇偶性,并说明理由
的奇偶性,并说明理由
(2)讨论函数![]() 的零点个数
的零点个数
【答案】(1)既不是奇函数也不是偶函数(2)见解析
【解析】
(1)先确定定义域,再研究![]() 与
与![]() 关系,讨论函数奇偶性;(2)利用分离变量法化为函数,根据绝对值定义化为分段函数,结合函数图像确定函数零点个数
关系,讨论函数奇偶性;(2)利用分离变量法化为函数,根据绝对值定义化为分段函数,结合函数图像确定函数零点个数
(1)当m=0时,函数f(x)=|x|﹣3,此时f(﹣x)=f(x)函数是偶函数;当m≠0时,∵f(1)=m﹣2,f(﹣1)=﹣m﹣2,∴f(﹣1)≠±f(1),函数是非奇非偶函数.
(2)由f(x)=0可得x|x|﹣3x+m=0(x≠0),
变为m=﹣x|x|+3x(x≠0)
令g(x)=3x﹣x|x|=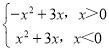
=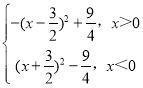 ,
,
作函数y=g(x)以及y=m的图象,可得:作y=g(x)的图象及直线y=m,由图象可得:
当m>![]() 或m<﹣
或m<﹣![]() 时,f(x)有1个零点.
时,f(x)有1个零点.
当m=![]() 或m=0或m=﹣
或m=0或m=﹣![]() 时,f(x)有2个零点;
时,f(x)有2个零点;
当0<m<![]() 或﹣
或﹣![]() <m<0时,f(x)有3个零点.
<m<0时,f(x)有3个零点.
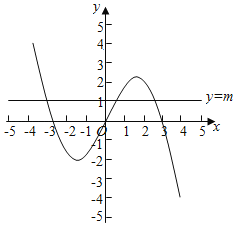

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
