题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)证明:当![]() 时,
时,![]() ;
;
(2)若![]() 时不等式
时不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)构造函数![]() 求导分析单调性证明
求导分析单调性证明![]() 即可.
即可.
(2)构造函数![]() ,求导后根据区间端点和极值点的大小关系等分参数的范围进行分析最大值即可.
,求导后根据区间端点和极值点的大小关系等分参数的范围进行分析最大值即可.
解:(1)令![]() ,
,
![]() ,
,
所以当![]() 时,
时,![]() 单调递减.
单调递减.
当![]() 时,
时,![]() 单调递减.
单调递减.
![]() 当
当![]() 时,
时,![]() 取得最大值,
取得最大值,
![]() ,
,
即![]() ,
,
![]() 当
当![]() 时,
时,![]() .
.
(2)令![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() 满足题意.
满足题意.
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(ⅰ)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() ,此时无解.
,此时无解.
(ⅱ)当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
所以![]() .
.
设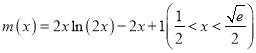 ,则
,则![]() ,
,
所以![]() 在
在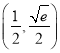 上单调递增,
上单调递增,
![]() ,不满足题意.
,不满足题意.
(ⅲ)当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,所以
,所以![]() 满足题意.
满足题意.
综上所述:![]() 的取值范围为
的取值范围为![]() .
.

【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收费比率 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
该公司注册的会员中没有消费超过5次的,从注册的会员中,随机抽取了100位进行统计,得到统计数据
如下:
消费次数 | 1次 | 2次 | 3次 | 4次 | 5次 |
人数 | 60 | 20 | 10 | 5 | 5 |
假设汽车美容一次,公司成本为150元,根据所给数据,解答下列问题:
(1)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(2)以事件发生的频率作为相应事件发生的概率, 设该公司为一位会员服务的平均利润为![]() 元,求
元,求![]() 大于40的概率.
大于40的概率.
【题目】某校将一次测试中高三年级学生的数学成绩统计如下表所示,在参加测试的学生中任取1人,其成绩不低于120分的概率为![]() .
.
分数 |
|
|
|
|
|
|
|
频数 | 40 | 50 | 70 | 60 | 80 |
| 50 |
(1)求![]() 的值;
的值;
(2)若按照分层抽样的方法从成绩在![]() 、
、![]() 的学生中抽取6人,再从这6人中随机抽取2人进行错题分析,求这2人中至少有1人的分数在
的学生中抽取6人,再从这6人中随机抽取2人进行错题分析,求这2人中至少有1人的分数在![]() 的概率.
的概率.