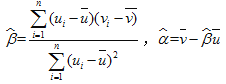题目内容
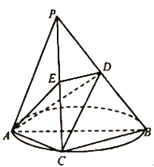
【题目】如图甲，AD，BC是等腰梯形CDEF的两条高，
，点M是线段AE的中点，将该等腰梯形沿着两条高AD，BC折叠成如图乙所示的四棱锥P-ABCD（E，F重合，记为点P）.
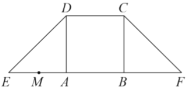
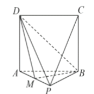
甲 乙
（1）求证：
；
（2）求点M到平面BDP距离h.
【答案】（1）证明见解析 （2）
【解析】
（1）先证明
平面ADP，再证明
即可；
（2）利用等体积法，由
，然后结合锥体体积公式求解即可.
解：（1）因为
，所以
，
又
，AP，
平面ABP，
所以
平面ABP，
因为
平面ABP，所以
；
由已知得，
，
所以
是等边三角形，
又因为点M是AP的中点，所以
；
因为
平面ADP，
所以平面ADP，
因为
平面ADP，
所以.
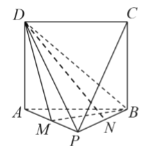
（2）取BP中点N，连结DN，
因为平面ABP，
，
所以
，所以
，
所以，在
中，
，
所以
，
因为平面ABP，
所以
，
因为，
所以
，
又
，
所以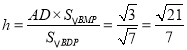
，
即点M到平面BDP的距高为.
练习册系列答案
期末集结号系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的年宣传费
和年销售量
（
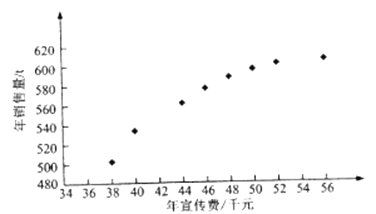
=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中
，
=
（Ⅰ）根据散点图判断，y=a+bx与y=c+d
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据（Ⅱ）的结果回答下列问题：
（ⅰ）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ⅱ）年宣传费x为何值时，年利率的预报值最大？
附：对于一组数据
,
，……，
,其回归线
的斜率和截距的最小二乘估计分别为：
