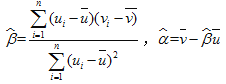题目内容
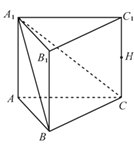
【题目】在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
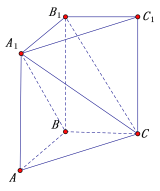
(1)求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
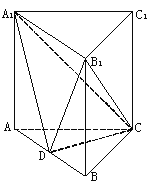
以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() .
.
(1)利用空间向量法求出![]() 与
与![]() 所成角的余弦值,再利用同角三角函数的基本关系可得出答案;
所成角的余弦值,再利用同角三角函数的基本关系可得出答案;
(2)利用空间向量法求出直线![]() 与平面
与平面![]() 所成角的正弦值,再利用同角三角函数的基本关系可得出答案.
所成角的正弦值,再利用同角三角函数的基本关系可得出答案.
在直三棱柱![]() 中,
中,![]() ,以点
,以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如下图所示:
,如下图所示:
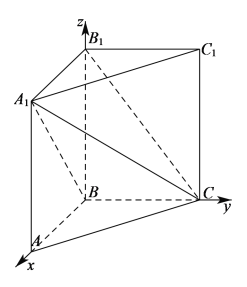
则点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,![]() ,
,![]() ,
,
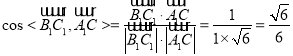 ,即
,即![]() ,
,![]() ,
,
则![]() ,因此,异面直线
,因此,异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
(2)设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,设平面
,设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由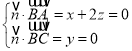 ,得
,得![]() ,取
,取![]() ,得
,得![]() ,
,
所以,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
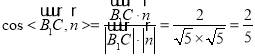 ,
,![]() ,则
,则![]() .
.
因此,直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.

 名校课堂系列答案
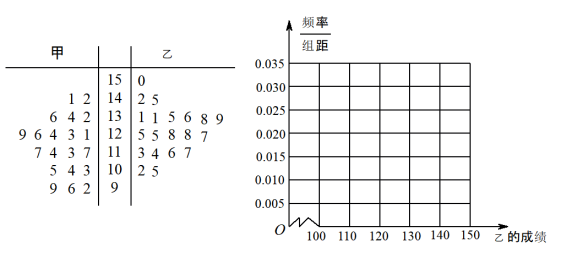
名校课堂系列答案【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:![]() ,
,![]() ;
;![]()
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
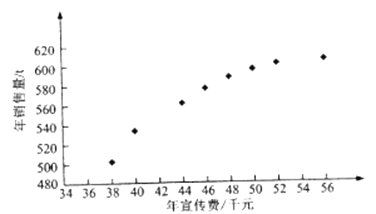
(![]() =1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
46.6 | 56.3 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
,![]() =
=![]()
![]()
(Ⅰ)根据散点图判断,y=a+bx与y=c+d![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给判断即可,不必说明理由)
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利率z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(ⅰ)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费x为何值时,年利率的预报值最大?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: