题目内容
【题目】己知函数
，
，
.
（1）讨论函数
的单调性；
（2）若
在
处取得极大值，求
的取值范围.
【答案】(1) 
在
上是递增的，在
上是递减的.(2) 
.
【解析】
(1)首先求得导函数的解析式，然后结合函数的定义域分类讨论函数的单调性即可；
(2)由题意结合(1)的结论可知
，据此结合导函数的解析式分类讨论即可确定实数a的取值范围.
（1）∵
∴
∵
①当
时，
∴在
上是递增的
②当
时，若
，则，若
，则
∴在上是递增的，在上是递减的.
（2）∵
，∴
由（1）知：
①当
时，
在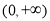上是递增的，
若
，则
，若
，则
∴
在
取得极小值，不合题意
②
时，在
上是递增的，在
上是递减的，
∴
∴在上是递减的
∴无极值，不合题意.
③当
时，
，由（1）知: 在上是递增的，
∵
∴若，则，若
，则，
∴在处取得极小值，不合题意.
④当
时，
，由（1）知: 在上是递减的，
∵
∴若
，则，若），则，
∴在
上是递增的，在上是递减的，
故在处取得极大值，符合题意.
综上所述:.
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：万元）对年销售量
（单位：吨）和年利润
（单位：万元）的影响．对近六年的年宣传费
和年销售量
（
）的数据作了初步统计，得到如下数据：
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟，发现年宣传费（万元）与年销售量（吨）之间近似满足关系式
（
）．对上述数据作了初步处理，得到相关的值如表：
|
|
|
|
|
|
|
|
（1）根据所给数据，求关于的回归方程；
（2）已知这种产品的年利润与，的关系为
若想在
年达到年利润最大，请预测年的宣传费用是多少万元？
附：对于一组数据
，
，…，
，其回归直线
中的斜率和截距的最小二乘估计分别为
，
【题目】某财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象．为了研究使用淡化海砂与混凝土耐久性是否达标有关，某大学实验室随机抽取了60个样本，得到了相关数据如下表：
混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 | |
使用淡化海砂 | 25 | t | 30 |
使用未经淡化海砂 | s | 15 | 30 |
总计 | 40 | 20 | 60 |
（Ⅰ）根据表中数据，求出s，t的值，利用独立性检验的方法判断，能否在犯错误的概率不超过1%的前提下认为使用淡化海砂与混凝土耐久性是否达标有关？
（Ⅱ）若用分层抽样的方法在使用淡化海砂的样本中抽取了6个，现从这6个样本中任取2个，则取出的2个样本混凝土耐久性都达标的概率是多少？
参考数据：
P（K2≥k0） | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式：
．
