题目内容
【题目】在三棱柱
中，侧棱与底面垂直，
，
，
，点
是
的中点．
（1）求证：
平面
；
（2）求证：
.
【答案】（1）见解析； （2）见解析.
【解析】
（1）设CB1与C1B的交点为E，连接DE，根据D是AB的中点，E是BC1的中点，可知DE∥AC1，而DE平面CDB1，AC1平面CDB1，根据线面平行的判定定理可知AC1∥平面CDB1；
（2）三棱柱ABC-A1B1C1中，底面三边长AC，BC，AB满足勾股定理则AC⊥BC，又侧棱垂直于底面ABC，则CC1⊥AC，又BC∩CC1=C，根据线面垂直的判定定理可知AC⊥面BB1C1C又B1C 平面BCC1，根据线面垂直的性质可知AC⊥BC1．
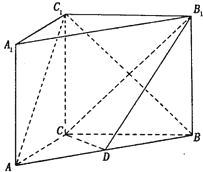
⑴连接BC1交B1C与点O，连接OD.
∵四边形BB1C1C为矩形，∴点O为BC1的中点.
又∵点D为BA的中点 ∴OD∥AC1 ∵OD
平面CDB1，AC1
平面CDB1
∴AC1∥平面CDB1 .
（2）∵
∴AC⊥BC,
∵CC1⊥平面ABC, 
，
又
CC1∩BC=C ∴AC⊥面BB1C1C
∵B1C面BB1C1C ∴
.
练习册系列答案
科学实验活动册系列答案
相关题目
