题目内容
19．已知a为常数，y=|x-a|-|x+a|最大值为M，最小值为N，且M-N=12，则实数a的值为（ ）| A． | 6 | B． | ±6 | C． | 3 | D． | ±3 |
分析 根据绝对值的性质，||a|-|b||≤|a-b|，可得-|-2a|≤y≤|-2a|，结合y的最大值为M，最小值为N，且M-N=12，可得答案．
解答 解：根据绝对值的性质，||a|-|b||≤|a-b|，
可得：|y|=||x-a|-|x+a||≤|（x-a）-（x+a）|=|-2a|，
故-|-2a|≤y≤|-2a|，
即M=|-2a|，N=-|-2a|，
由M-N=12得：|-4a|=12，解得：a=±3，
故选：D
点评 本题考查的知识点是绝对值的性质，熟练掌握||a|-|b||≤|a-b|，是解答的关键．
练习册系列答案
相关题目
10．x2-y2cosθ=1，其中θ∈（π，$\frac{3}{2}$π），则方程所表示的曲线为（ ）
| A． | 焦点在x轴上的椭圆 | B． | 焦点在y轴上的椭圆 | ||
| C． | 焦点在x轴上的双曲线 | D． | 表示焦点在y轴上的双曲线 |
10．函数f（x）=ax+loga（x+1）在[0，1]上的最大值与最小值之和为a，则a的值为（ ）
| A． | $\frac{1}{4}$ | B． | 4 | C． | $\frac{1}{2}$ | D． | 2 |
7．已知f（x）=cosx，且f1（x）=f′（x），fn+1（x）=fn′（x）（n∈N*），则f2015（x）=（ ）
| A． | -sin x | B． | -cos x | C． | sin x | D． | cos x |
14．若点P的坐标为（x0，y0），曲线C的方程为F（x，y）=0，则“F（x0，y0）=0”是“点P在曲线C上”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
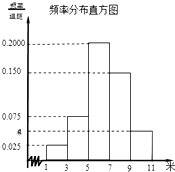为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成[1，3），[3，5），[5，7），[7，9），[9，11]五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
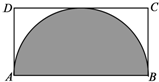如图所示，在矩形ABCD中，AB=2a，AD=a，图中阴影部分是以AB为直径的半圆，现在向矩形ABCD内随机撒4000粒豆子（豆子的大小忽略不计），根据你所学的概率统计知识，下列四个选项中最有可能落在阴影部分内的豆子数目是（ ）