题目内容
选修42:矩阵与变换
已经矩阵M=.
(1)求直线4x-10y=1在M作用下的方程;
(2)求M的特征值与特征向量.
已经矩阵M=.
(1)求直线4x-10y=1在M作用下的方程;
(2)求M的特征值与特征向量.
(1) 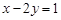 .
.
(2)当λ1=4时,由Mα1=λ1α1,得特征向量α1=;
当λ2=5时,由Mα2=λ2α2,得特征向量α2=.
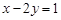 .
. (2)当λ1=4时,由Mα1=λ1α1,得特征向量α1=;
当λ2=5时,由Mα2=λ2α2,得特征向量α2=.
本试题主要是考查了矩阵的运算,以及特征向量的求解和特征多项式的表示的综合运用。
(1)因为M=.设直线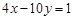 上任意一点
上任意一点 在作用下对应点
在作用下对应点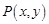 ,则 = ,
,则 = ,
(2)因为矩阵M的特征多项式f(λ)==(λ-4)(λ-5)=0,进而讨论得到特征向量。
(1)因为M=. 设直线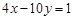 上任意一点
上任意一点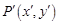 在作用下对应点
在作用下对应点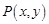 ,则 = ,………………………………………………………………2分
,则 = ,………………………………………………………………2分
即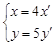 ,所以
,所以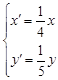 ,代入
,代入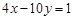 ,得
,得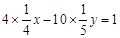 ,即
,即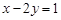 ,
,
所以所求曲线的方程为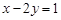 .……………………………………………………………4分
.……………………………………………………………4分
(2)矩阵M的特征多项式f(λ)==(λ-4)(λ-5)=0,
所以M的特征值为λ1=4,λ2=5. …………………………………………………………6分
当λ1=4时,由Mα1=λ1α1,得特征向量α1=;
当λ2=5时,由Mα2=λ2α2,得特征向量α2=.…………………………………………10分
(1)因为M=.设直线
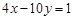 上任意一点
上任意一点 在作用下对应点
在作用下对应点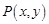 ,则 = ,
,则 = ,(2)因为矩阵M的特征多项式f(λ)==(λ-4)(λ-5)=0,进而讨论得到特征向量。
(1)因为M=. 设直线
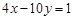 上任意一点
上任意一点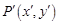 在作用下对应点
在作用下对应点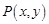 ,则 = ,………………………………………………………………2分
,则 = ,………………………………………………………………2分即
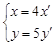 ,所以
,所以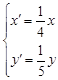 ,代入
,代入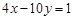 ,得
,得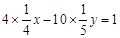 ,即
,即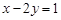 ,
,所以所求曲线的方程为
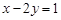 .……………………………………………………………4分
.……………………………………………………………4分(2)矩阵M的特征多项式f(λ)==(λ-4)(λ-5)=0,
所以M的特征值为λ1=4,λ2=5. …………………………………………………………6分
当λ1=4时,由Mα1=λ1α1,得特征向量α1=;
当λ2=5时,由Mα2=λ2α2,得特征向量α2=.…………………………………………10分

练习册系列答案
相关题目
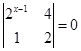 ,则
,则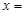 .
.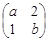 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量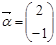 .
.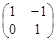 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求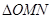 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的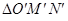 的面积.
的面积. 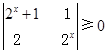 的解为 .
的解为 . ,并且矩阵
,并且矩阵 对应的变换将点
对应的变换将点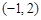 变成点
变成点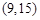 ,求出矩阵
,求出矩阵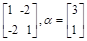 ,试计算
,试计算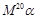
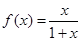 ,在9行9列的矩阵
,在9行9列的矩阵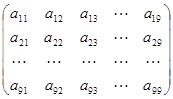 中,第
中,第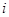 行第
行第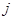 列的元素
列的元素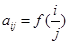 ,则这个矩阵中所有数之和为_______________.
,则这个矩阵中所有数之和为_______________. 所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中
所做的前两题计分。作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将选题号填入括号中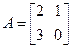 的特征值及对应的特征向量。
的特征值及对应的特征向量。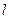 的参数方程:
的参数方程: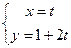 (
(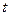 为参数)和圆
为参数)和圆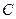 的极坐标方程:
的极坐标方程: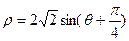 。
。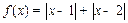 . 若不等式
. 若不等式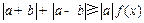
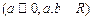 恒成立,求实数
恒成立,求实数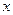 的范围。
的范围。 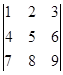 中元素8的代数余子式为______________.
中元素8的代数余子式为______________.