题目内容
已知矩阵A=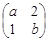 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量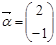 .
.
(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=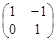 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求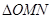 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的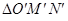 的面积.
的面积.
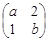 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量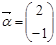 .
.(Ⅰ) 求矩阵A;
(Ⅱ) 矩阵B=
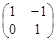 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求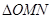 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的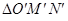 的面积.
的面积. (A)=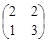 .(2)8
.(2)8
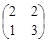 .(2)8
.(2)8试题分析:Ⅰ)由已知得
 ,所以
,所以 2分
2分解得
 故A=
故A=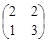 . 3分
. 3分(Ⅱ) AB=
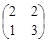
 =
= ,所以
,所以 ,
, ,
, 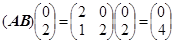 ,5分
,5分即点O,M,N变成点O′(0,0),M′(4,0),N′(0,4),
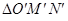 的面积为
的面积为 .7分
.7分点评:主要是考查矩阵的变换以及对应的三角形的面积计算,考查了基本的运算能力,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
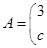
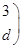 ,若矩阵
,若矩阵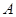 属于特征值6的一个特征向量为
属于特征值6的一个特征向量为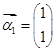 ,属于特征值1的一个特征向量
,属于特征值1的一个特征向量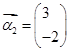 .
.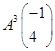
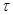 :
: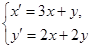 对应的矩阵为
对应的矩阵为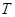 ,向量β
,向量β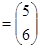 .
.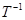 ;
;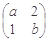 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量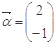 .
.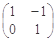 ,求直线
,求直线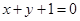 先在矩阵A,再在矩阵B的对应变换作用下的像的方程.
先在矩阵A,再在矩阵B的对应变换作用下的像的方程. 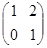 ,B-1 =
,B-1 =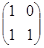 ,则 (AB)-1 = ;
,则 (AB)-1 = ;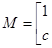
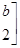 有特征值
有特征值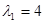 及对应的一个特征向量
及对应的一个特征向量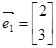 ,求曲线
,求曲线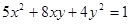 在
在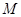 的作用下的新曲线方程.
的作用下的新曲线方程.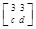 ,若矩阵A属于特征值6的一个特征向量为α1=
,若矩阵A属于特征值6的一个特征向量为α1=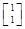 ,属于特征值1的一个特征向量为α2=
,属于特征值1的一个特征向量为α2=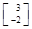 .求矩阵A,并写出A的逆矩阵.
.求矩阵A,并写出A的逆矩阵.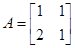 ,向量
,向量 ,求向量
,求向量 ,使得
,使得 .
.