题目内容
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点. 求证: 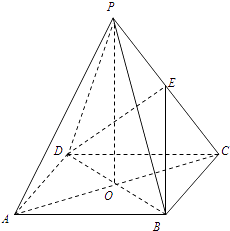
(1)PA∥平面BDE;
(2)BD⊥平面PAC.
【答案】
(1)证明:连接OE,

在△CAP中,CO=OA,CE=EP,
∴PA∥EO,
又∵PA平面BDE,EO平面BDE,
∴PA∥平面BDE
(2)证明∵PO⊥底面ABCD,BD平面ABCD,
∴BD⊥PO
又∵四边形ABCD是正方形,
∴BD⊥AC
∵AC∩PO=O,AC,PO平面PAC
∴BD⊥平面PAC
【解析】(1)连接OE,根据三角形中位线定理,可得PA∥EO,进而根据线面平行的判定定理,得到PA∥平面BDE.(2)根据线面垂直的定义,可由PO⊥底面ABCD得到BD⊥PO,结合四边形ABCD是正方形及线面垂直的判定定理可得BD⊥平面PAC
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
相关题目