题目内容
已知函数f(x)=
sin(2ωx-
)+b，且该函数图象的对称中心和对称轴的最小距离为
，当x∈[0，
]时，f（x）的最大值为
．
（1）求f（x）的解析式．
（2）画出f（x）在长度为一个周期内的简图（直接画图，不用列表）．
（3）分步说明该函数的图象是由正弦曲线经过怎样的变化得到的．
| 3 |
| π |
| 3 |
| π |
| 4 |
| π |
| 3 |
| 5 |
| 2 |
（1）求f（x）的解析式．
（2）画出f（x）在长度为一个周期内的简图（直接画图，不用列表）．
（3）分步说明该函数的图象是由正弦曲线经过怎样的变化得到的．
分析：（1）由函数图象的对称中心和对称轴的最小距离为
，得周期，从而可得ω，由最大值可得b；
（2）用五点法可作得函数图象；
（3）根据图象的变化规律可逐步得到；
| π |
| 4 |
（2）用五点法可作得函数图象；
（3）根据图象的变化规律可逐步得到；
解答：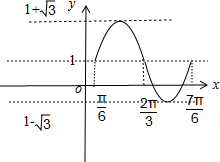
解：（1）∵该函数图象的对称中心和对称轴的最小距离为
，
∴最小正周期T=π，则ω=1，
当x∈[0，
]时，2x-
∈[-
，
]，
∴f（x）max=
×
+b=
，解得b=1，
∴f（x）=
sin(2x-
)+1；
（2）函数f（x）的图象如右：
（3）把函数y=sinx的图象向右平移
个单位得到y=sin（x-
）的图象，纵坐标不变，横坐标缩短为原来的
倍，
得到y=sin（2x-
）的图象，横坐标不变，纵坐标伸长为原来的
倍，得到y=
sin（x-
）的图象，
再把图象上所有点向上平移1个单位，得到f（x）=
sin(2x-
)+1的图象．
解：（1）∵该函数图象的对称中心和对称轴的最小距离为| π |
| 4 |
∴最小正周期T=π，则ω=1，
当x∈[0，
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f（x）max=
| 3 |
| ||
| 2 |
| 5 |
| 2 |
∴f（x）=
| 3 |
| π |
| 3 |
（2）函数f（x）的图象如右：
（3）把函数y=sinx的图象向右平移
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
得到y=sin（2x-
| π |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
再把图象上所有点向上平移1个单位，得到f（x）=
| 3 |
| π |
| 3 |
点评：本题考查y=Asin（ωx+φ）+b的图象作法、图象变换及函数解析式的求解，属中档题．
练习册系列答案
相关题目