题目内容
9.已知正三角形ABC的边长为2$\sqrt{3}$,○O是该三角形的内切圆,P是圆O上的任意一点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最大值为1.分析 结合图形,利用向量数量积公式把$\overrightarrow{PA}$•$\overrightarrow{PB}$化为三角函数形式,利用和差化积公式化为一个角的三角函数,根据三角函数的值域求得最大值.
解答 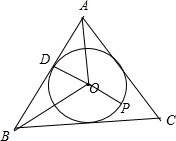 解:如图所示,由正△ABC边长等于2$\sqrt{3}$,点P在其内切圆上运动.
解:如图所示,由正△ABC边长等于2$\sqrt{3}$,点P在其内切圆上运动.
∴∠AOB=120°,设AB的中点为D,则半径r=OD=$\frac{AD}{tan∠AOD}$=$\frac{\sqrt{3}}{tan60°}$=1.
OA=OB=0C=2r=2.
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=($\overrightarrow{OA}-\overrightarrow{OP}$)•($\overrightarrow{OB}-\overrightarrow{OP}$)=$\overrightarrow{OA}•\overrightarrow{OB}$-$\overrightarrow{OA}•\overrightarrow{OP}$-$\overrightarrow{OP}•\overrightarrow{OB}$+${\overrightarrow{OP}}^{2}$
=$\overrightarrow{OA}•\overrightarrow{OB}$-$\overrightarrow{OP}$•2$\overrightarrow{OD}$+1
=2×2×cos120°-1×2×cos<$\overrightarrow{OP}$,$\overrightarrow{OD}$>+1
=-1-2•cos<$\overrightarrow{OP}$,$\overrightarrow{OD}$>,
故当<$\overrightarrow{OP}$,$\overrightarrow{OD}$>=π 时,$\overrightarrow{PA}$•$\overrightarrow{PB}$的最大值为-1+2=1,
故答案为:1.
点评 本题考查了向量的数量积公式,正弦定理及三角函数的和差化积公式,数形结合是解答本题的关键,属于中档题.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案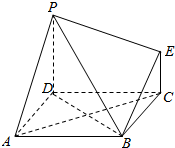 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且