题目内容
3.设函数f(x)=lnx-x2+x+a(a∈R,e是自然对数的底数)(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若关于x的方程f(x)=x2+x+2在区间[$\frac{1}{e}$,e]上恰有两相异实根,求a的取值范围;
(Ⅲ)当a≤2时,证明:f(x)-ex-1<0.
分析 (I)由f′(x)=$\frac{1}{x}$-2x+1,x>0,知当0<x<1时,f'(x)>0,f(x)单调递增;当x>1时,f'(x)<0,f(x)单调递减.由此能求出函数f(x)的单调区间.
(II)方程lnx-x2+x+a=x2+x+2化为a=2x2+2-lnx,令g(x)=2x2-2-lnx,由g(x)的单调性,结合在[1,e]上单调递增f(x)=x2-2x+2a在[$\frac{1}{e}$,e]上有两个相异实根,由此能列出关于a的不等关系求出实数a的取值范围,
(Ⅲ)要证原不等式成立,只需证明f(x)<ex+1成立,由(1)可知当x=1时,f(x)max=a≤2,继而得到ex>1,问题得以证明.
解答 解:(1)∵f(x)=lnx-x2+x+a,
∴f′(x)=$\frac{1}{x}$-2x+1=$\frac{-(2x+1)(x-1)}{x}$,
∴x>1时,f'(x)<0;0<x<1时,f'(x)>0
故f(x)的单调递减区间是(1,+∞),单调递增区间是(0,1)
(2)f(x)=x2+x+2得到lnx-x2+x+a=x2+x+2,即a=2x2+2-lnx,
令g(x)=2x2-2-lnx,
则g′(x)=4x-$\frac{1}{x}$=$\frac{4(x-\frac{1}{2})(x+\frac{1}{2})}{x}$
当x∈[$\frac{1}{e}$,$\frac{1}{2}$)时,g′(x)<0,g(x)递减
当x∈($\frac{1}{2}$,e]时,g′(x)>0,g(x)递增
又g($\frac{1}{2}$)=ln2-$\frac{3}{2}$,g($\frac{1}{e}$)=$\frac{2}{{e}^{2}}$-1,g(e)=2e2-3,
∵g($\frac{1}{e}$)<g(e),
∴ln2-$\frac{3}{2}$<a≤$\frac{2}{{e}^{2}}$-1,
(3)要证原不等式成立,只需证明f(x)<ex+1成立
由(1)可知当x=1时,f(x)max=a≤2,
又x>0时,ex>1,
∴ex+1>2,
故f(x)<ex+1,
即当a≤2时,f(x)-ex-1<0.
点评 本题考查导数的性质和应用、利用导数研究函数的单调性,具有一定的难度,解题时要注意挖掘题设中的隐含条件,属于中档题.

| 作物产量(kg) | 300 | 500 |
| 概率 | 0.5 | 0.5 |
| 作物市场价格(元/kg) | 6 | 10 |
| 概率 | 0.6 | 0.4 |
(Ⅱ)若在这块地上连续3年种植此作物,求这3年中第二年的利润少于第一年的概率.

| A. | 8-$\frac{π}{6}$ | B. | 8-$\frac{π}{4}$ | C. | 8-$\frac{π}{3}$ | D. | 8-$\frac{π}{2}$ |
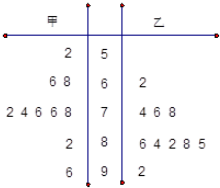
| A. | a1<a2,s1>s2 | B. | a1<a2,s1<s2 | C. | a1>a2,s1>s2 | D. | a1>a2,s1<s2 |