题目内容
15.已知函数f(x)=$\frac{{e}^{x}}{x+1}$( e是自然对数的底数).(1)求函数f(x)的单调区间;
(2)当x1≠x2,f(x1)=f(x2)时,证明:x1+x2>0.
分析 (1)先求出函数的导数,通过解关于导函数的不等式,从而求出函数的单调区间;
(2)由题意得:若f(x1)=f(x2),x1≠x2,则必有x1,x2∈(-1,+∞),不妨设x1∈(-1,0),x2∈(0,+∞),若证x1+x2>0,即证x2>-x1>0,只需证:f(x2)>f(-x1),即证明$g(x)=\frac{e^x}{x+1}-\frac{{{e^{-x}}}}{1-x}>0$在x∈(-1,0)上恒成立,通过讨论g(x)的单调性即可证明.
解答 解:(1)由f(x)=$\frac{{e}^{x}}{x+1}$(x≠-1)得:$f'(x)=\frac{{x{e^x}}}{{{{(x+1)}^2}}}$,x≠-1,
令f′(x)>0得:x>0,令f′(x)<0得:x<0,x≠-1,
所以函数f(x)的单调增区间为(0,+∞),单调减区间为(-∞,-1),(-1,0).
(2)由(1)知,当x∈(-∞,-1)时,f(x)<0;当x∈(-1,+∞)时,f(x)>0,
则f(x)在(-1,0)为减函数,在(0,+∞)为增函数,
若f(x1)=f(x2),x1≠x2,则必有x1,x2∈(-1,+∞),
不妨设x1∈(-1,0),x2∈(0,+∞).
若证x1+x2>0,即证x2>-x1>0,只需证:f(x2)>f(-x1)
即:f(x1)>f(-x1),设g(x)=f(x)-f(-x),x∈(-1,0),
即$g(x)=\frac{e^x}{x+1}-\frac{{{e^{-x}}}}{1-x}>0$在x∈(-1,0)上恒成立,
即(1-x)e2x-(1+x)>0.
设h(x)=(1-x)e2x-(1+x),x∈(-1,0)h′(x)=e2x(1-2x)-1,(h′(x)′=-4xe2x>0,
∴h′(x)是(-1,0)上的增函数,故h′(x)<h′(0)=0,
∴h(x)是(-1,0)上是减函数,故h(x)>h(0)=0,所以原命题成立.
点评 本题考察了函数的单调性,导数的应用,考察函数恒成立问题,通过证明$g(x)=\frac{e^x}{x+1}-\frac{{{e^{-x}}}}{1-x}>0$在x∈(-1,0)上恒成立是解答(2)的关键,本题是一道难题.

| A. | 相交 | B. | 平行 | C. | 异面 | D. | 垂直 |
(1)下面摘取了随机数表的第7行到第9行
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 66 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
如果从第8行第7列的数开始向右读,请你依次写出最先检查的5个人的编号;
(2)抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向、纵向分别表示地理成绩与数学成绩各等级人数,例如:表中数学成绩为良好的共有20+18+4=42.在该样本中,数学成绩优秀率是30%,
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
| A. | $-\frac{1}{5}$ | B. | $-\frac{i}{5}$ | C. | $\frac{2i}{5}$ | D. | $\frac{2}{5}$ |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
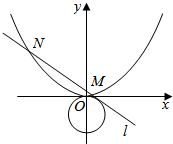 已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).
已知抛物线的顶点在坐标原点,焦点在y轴上,且过点(2,1).