题目内容
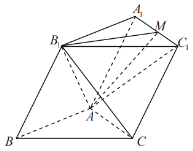
【题目】已知平面四边形ABCD是菱形,![]() ,
,![]() ,将
,将![]() 沿对角线BD翻折至
沿对角线BD翻折至![]() 的位置,且二面角
的位置,且二面角![]() 的平面角为
的平面角为![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积为( )
的外接球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
设![]() ,由四边形ABCD是菱形,可得
,由四边形ABCD是菱形,可得![]() 为二面角
为二面角![]() 的平面角,故
的平面角,故![]() .过三棱锥
.过三棱锥![]() 的外接球的球心
的外接球的球心![]() 作
作![]() 面
面![]() ,垂足为
,垂足为![]() ,则
,则![]() 是等边
是等边![]() 的中心. 作
的中心. 作![]() ,垂足为
,垂足为![]() ,可证
,可证![]() 面
面![]() ,故
,故![]() .作
.作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是矩形. 设外接球的半径为
是矩形. 设外接球的半径为![]() ,则
,则![]() ,
,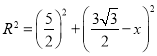 ,求出
,求出![]() ,即求
,即求![]() ,进而求出外接球的表面积.
,进而求出外接球的表面积.
设![]() ,
,![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,
![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() .
.
![]() 是等边三角形.
是等边三角形.
过三棱锥![]() 的外接球的球心
的外接球的球心![]() 作
作![]() 面
面![]() ,垂足为
,垂足为![]() ,
,
则![]() 是等边
是等边![]() 的中心.
的中心.
如图所示
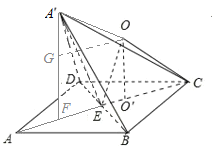
![]() .
.
设外接球的半径为![]() ,则
,则![]() .
.
作![]() ,垂足为
,垂足为![]() .
.
![]() 面
面![]() ,
,
即![]() 面
面![]() ,
,![]() .又
.又![]() ,
,
![]() 面
面![]() .
.
作![]() 交
交![]() 于点
于点![]() ,则四边形
,则四边形![]() 是矩形,
是矩形,![]() .
.
![]() .
.
![]() .
.
![]() .
.
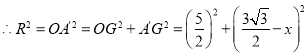 ,
,
又![]() ,
,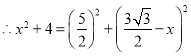 ,
,
解得![]() .
.
![]() 三棱锥
三棱锥![]() 的外接球的表面积
的外接球的表面积![]() .
.
故选:![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目