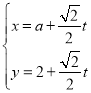题目内容
【题目】某景区平面图如图1所示,![]() 为边界上的点.已知边界
为边界上的点.已知边界![]() 是一段抛物线,其余边界均为线段,且
是一段抛物线,其余边界均为线段,且![]() ,抛物线顶点
,抛物线顶点![]() 到
到![]() 的距离
的距离![]() .以
.以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.
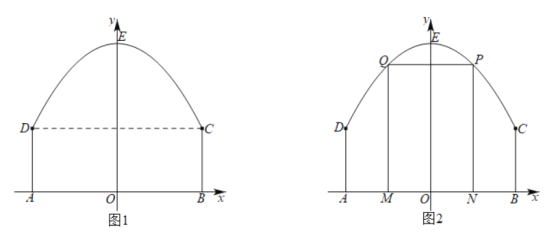
(1)求边界![]() 所在抛物线的解析式;
所在抛物线的解析式;
(2)如图2,该景区管理处欲在区域![]() 内围成一个矩形
内围成一个矩形![]() 场地,使得点
场地,使得点![]() 在边界
在边界![]() 上,点
上,点![]() 在边界
在边界![]() 上,试确定点
上,试确定点![]() 的位置,使得矩形
的位置,使得矩形![]() 的周长最大,并求出最大周长.
的周长最大,并求出最大周长.
【答案】(1)![]() ;(2)点
;(2)点![]() 与点
与点![]() 重合.最大值为22,
重合.最大值为22,
【解析】
(1)根据题意,设二次函数解析式为![]() ,代入点C、E坐标,即可求解参数;
,代入点C、E坐标,即可求解参数;
(2)根据题意结合(1)中抛物线解析式,设![]() 点坐标为
点坐标为![]() ,利用坐标表达矩形的周长,根据二次函数性质,可求最值问题.
,利用坐标表达矩形的周长,根据二次函数性质,可求最值问题.
(1)根据对称性可知,![]() ,
,
![]() ,
,
设边界![]() 所在抛物线的解析式为
所在抛物线的解析式为![]() ,
,
![]() 抛物线的图象经过
抛物线的图象经过![]() ,
,![]() 两点,
两点,
![]() ,解得
,解得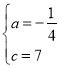 ,
,
![]() 边界
边界![]() 所在抛物线的解析式为
所在抛物线的解析式为![]() ;
;
(2)设![]() 点坐标为
点坐标为![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 矩形
矩形![]() 的周长为:
的周长为:
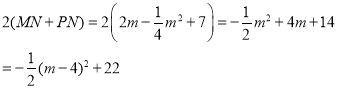
![]() ,开口向下,
,开口向下,
![]() 当
当![]() 时,矩形
时,矩形![]() 的周长有最大值,最大值为22,
的周长有最大值,最大值为22,
此时![]() 点坐标为
点坐标为![]() ,即点
,即点![]() 与点
与点![]() 重合.
重合.

练习册系列答案
相关题目