题目内容
6.已知向量$\overrightarrow{a}=(1,1),\overrightarrow{b}=(-2,x)$,若$\overrightarrow{a}=λ\overrightarrow{b}$(λ∈R),则x=( )| A. | $-\frac{1}{2}$ | B. | -2 | C. | 1 | D. | -1 |
分析 根据向量的坐标运算计算即可.
解答 解:∵向量$\overrightarrow{a}=(1,1),\overrightarrow{b}=(-2,x)$,$\overrightarrow{a}=λ\overrightarrow{b}$(λ∈R),
∴(1,1)=λ(-2,x),
∴$\left\{\begin{array}{l}{1=-2λ}\\{1=λx}\end{array}\right.$,
∴x=-2,
故选:B.
点评 本题考查了向量的坐标运算,属于基础题.

练习册系列答案
相关题目
16.在某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)预测该地区2016年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({t_i}-\bar\overline{t})({y_i}-\bar\overline{y})}}}{{\sum_{i=1}^n{{{({t_i}-\bar\overline{t})}^2}}}}$,$\hat a=\bar\overline{y}-\hat b\bar\overline{t}$.
| 年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)预测该地区2016年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\hat b=\frac{{\sum_{i=1}^n{({t_i}-\bar\overline{t})({y_i}-\bar\overline{y})}}}{{\sum_{i=1}^n{{{({t_i}-\bar\overline{t})}^2}}}}$,$\hat a=\bar\overline{y}-\hat b\bar\overline{t}$.
1.甲、乙两位射击运动员在一次射击测试中各射靶10次,两人射中环数统计结果如图所示:
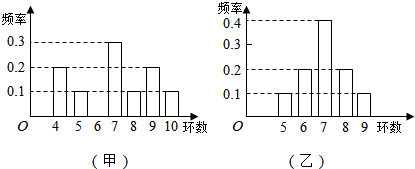
若用$\overline{x}$表示所得环数的平均数,s表示标准差,则下列结论正确的是( )

若用$\overline{x}$表示所得环数的平均数,s表示标准差,则下列结论正确的是( )
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$ | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | D. | s甲<s乙 |
11.定义数列{an},a1=1,当n≥2时,an=$\left\{\begin{array}{l}{{a}_{n-1},n=2k}\\{2{a}_{n-1},n=2k-1}\end{array}\right.$,k∈N*,Sn是其前n项和,则S10=( )
| A. | 61 | B. | 62 | C. | 31 | D. | 30 |
18.已知等差数列{an}中,a1+a2+a3+a4+a5=50,则a3=( )
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |