题目内容
13．变量 x，y 满足约束条件$\left\{\begin{array}{l}{x+2y≥2}\\{2x+y≤4}\\{4x-y≥-1}\end{array}\right.$，则z=2x-y的最大值为（ ）| A． | -1 | B． | 1 | C． | 4 | D． | 6 |
分析 先画出满足条件的平面区域，得到直线y=2x-z过（2，0）时z最大，从而求出答案．
解答 解：画出满足条件的平面区域，如图示：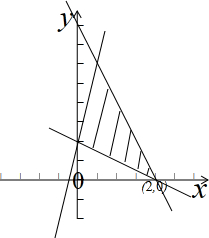
，
由z=2x-y得：y=2x-z，
∴直线y=2x-z过（2，0）时z最大，
Z最大值=4，
故选：C．
点评 本题考察了简单的线性规划问题，考察数形结合，是一道中档题．
练习册系列答案
相关题目
在四面体ABCD中，若AB=AD，CD=BC，求证：AC⊥BD．
如图，在正方体ABCD-A1B1C1D1中，点E是AB的中点，点F是AD的中点，求证：平面AA1C1C⊥平面A1EF．
8．设函数f（x）=exsinx-cosx，g（x）=xcosx-$\sqrt{2}$ex（其中e是自然对数的底数），?x1∈[0，$\frac{π}{2}$]，?x2∈[0，$\frac{π}{2}$]，使得不等式f（x1）+g（x2）≥m成立，则实数m的范围（ ）
| A． | （-∞，-1-$\sqrt{2}$] | B． | （-∞，${e}^{\frac{π}{2}}$-$\sqrt{2}$] | C． | （-∞，-1-$\sqrt{2}$${e}^{\frac{π}{2}}$] | D． | （-∞，（-1-$\sqrt{2}$）${e}^{\frac{π}{2}}$] |
12．
如图，在正方体ABCD-A1B1C1D1中，O1为底面的中心，则O1A与上底面A1B1C1D1所成角的正切值是（ ）
如图，在正方体ABCD-A1B1C1D1中，O1为底面的中心，则O1A与上底面A1B1C1D1所成角的正切值是（ ）| A． | 1 | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |