题目内容
18.设函数f(x)是偶函数,且在(-∞,0)上是增函数,判断f(x)在(0,+∞)上的单调性,并加以证明.分析 直接利用偶函数的性质:在关于原点对称的区间上单调性相反即可得出其在(0,+∞)上的单调性;再利用函数单调性的定义证明结论即可.
解答 解:因为偶函数在关于原点对称的区间上单调性相反;
且f(x)在(-∞,0)上是增函数,
故f(x)在(0,+∞)是减函数.
证明如下:若0<x1<x2<+∞,那么-∞<-x2<-x1<0.
由于偶函数在(-∞,0)上是增函数,故有:f(-x2)<f(-x1)
又根据偶函数的性质可得:f(-x1)=f(x1),f(-x2)=f(x2)
综上可得:f(x1)>f(x2)
故f(x)在(0,+∞)上是减函数
点评 本题主要考查函数奇偶性与单调性的综合问题.这一类型题目,主要是考查偶函数在关于原点对称的区间上单调性相反,而奇函数在关于原点对称的区间上单调性相同这一结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.函数f(x)=asin2x+b${x}^{\frac{2}{3}}$+c(a,b∈R),若f(-2015)=2013,则f(2015)=( )
| A. | 2018 | B. | -2009 | C. | 2013 | D. | -2013 |
6.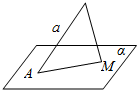 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )| A. | 线段 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
5.已知f(x)在定义域(-4,1)上是减函数,且f(1+a)<f(3a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |