题目内容
7. 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.给出下列四个命题:
①若p=q=0,则“距离坐标”为(0,0)的点有且仅有1个.
②若pq=0,且p+q≠0,则“距离坐标”为(p,q)的点有且仅有2个.
③若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个.
④若p=q,则点M的轨迹是一条过O点的直线.
其中所有正确命题的序号为①②③.
分析 根据点M的“距离坐标”的定义即可判断出正误.
解答 解:①若p=q=0,则“距离坐标”为(0,0)的点是两条直线的交点O,因此有且仅有1个,正确.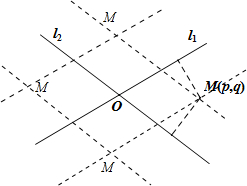
②若pq=0,且p+q≠0,则“距离坐标”为(0,q)(q≠0)或(p,0)(p≠0),因此满足条件的点有且仅有2个,
正确.
③若pq≠0,则“距离坐标”为(p,q)的点有且仅有4个,如图所示,正确.
④若p=q,则点M的轨迹是两条过O点的直线,分别为交角的平分线所在直线,因此不正确.
综上可得:只有①②③正确.
故答案为:①②③.
点评 本题考查了新定义“距离坐标”,考查了理解能力与推理能力、数形结合的思想方法,属于中档题.

练习册系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}(x≥0)}\\{lo{g}_{3}(-x)(x<0)}\end{array}\right.$,函数g(x)=[f(x)]2+f(x)+t,t∈R,则下列判断不正确的是( )
| A. | 若t=$\frac{1}{4}$,则g(x)有一个零点 | B. | 若-2<t<$\frac{1}{4}$,则g(x)有两个零点 | ||
| C. | 若t<-2,则g(x)有四个零点 | D. | 若t=-2,则g(x)有三个零点 |
15.设全集U=R,集合P={x|x2-x-6≥0},Q={x|2x≥1},则(CRP)∩Q=( )
| A. | {x|-2<x<3} | B. | {x|x≥0} | C. | {x|0≤x<3} | D. | {x|0≤x<2} |
2.定义在R上的函数f(x)满足f(x+6)=f(x).当x∈[-3,-1)时,f(x)=-(x+2)2,当x∈[-1,3)时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2015)=( )
| A. | 336 | B. | 355 | C. | 1676 | D. | 2015 |
19.已知i是虚数单位,$\overline{z}$是z=1+i的共轭复数,则$\frac{\overline{z}}{{z}^{2}}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.设a,b∈R,关于x,y的不等式|x|+|y|<1和ax+4by≥8无公共解,则ab的取值范围是( )
| A. | [-16,16] | B. | [-8,8] | C. | [-4,4] | D. | [-2,2] |
17.在极坐标系中,已知点$A(4,1),B(3,1+\frac{π}{2})$,则线段AB的长度是( )
| A. | 1 | B. | $\sqrt{1+\frac{π^2}{4}}$ | C. | 7 | D. | 5 |