题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{x}(x≥0)}\\{lo{g}_{3}(-x)(x<0)}\end{array}\right.$,函数g(x)=[f(x)]2+f(x)+t,t∈R,则下列判断不正确的是( )| A. | 若t=$\frac{1}{4}$,则g(x)有一个零点 | B. | 若-2<t<$\frac{1}{4}$,则g(x)有两个零点 | ||
| C. | 若t<-2,则g(x)有四个零点 | D. | 若t=-2,则g(x)有三个零点 |
分析 由题意作函数f(x)=$\left\{\begin{array}{l}{{3}^{x}(x≥0)}\\{lo{g}_{3}(-x)(x<0)}\end{array}\right.$的图象,再讨论t以确定[f(x)]2+f(x)+t=0的解与解的位置,从而结合图象解得.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{{3}^{x}(x≥0)}\\{lo{g}_{3}(-x)(x<0)}\end{array}\right.$的图象如下,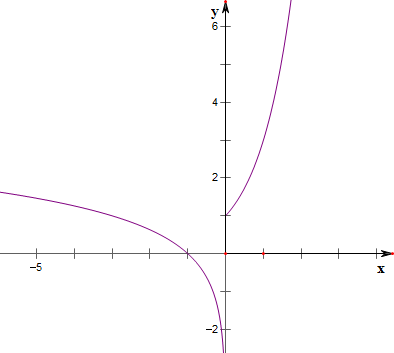
当t=$\frac{1}{4}$时,由[f(x)]2+f(x)+t=0得f(x)=-$\frac{1}{2}$,
故结合图象知g(x)有一个零点;
当-2<t<$\frac{1}{4}$时,[f(x)]2+f(x)+t=0有两个根,
其中一根小于-$\frac{1}{2}$,另一根大于-$\frac{1}{2}$且小于1;
故结合图象知g(x)有两个零点;
当t<-2时,[f(x)]2+f(x)+t=0有两个根,
其中一根小于-$\frac{1}{2}$,另一根大于1;
故结合图象知g(x)有三个零点;
故C不正确,
故选:C.
点评 本题考查了分段函数的应用及方程的根与函数的零点的关系应用,同时考查了数形结合的思想应用,属于中档题.

练习册系列答案
相关题目
7.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≤1}\\{x+1≥0}\\{x-y≤1}\end{array}\right.$,则目标函数z=$\frac{y}{x-2}$的取值范围为( )
| A. | [-3,3] | B. | [-2,2] | C. | [-1,1] | D. | [-$\frac{2}{3}$,$\frac{2}{3}$] |
12.设点P在曲线y=x2+1(x≥0)上,点Q在曲线y=$\sqrt{x-1}$(x≥1)上,则|PQ|的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
2.二项式(2x-$\frac{1}{2x}$)8的展开式的常数项是( )
| A. | -70 | B. | 64 | C. | 70 | D. | -32 |
9.若(x2+$\frac{a}{x}$)5的二项展开式中x7的系数为-10,则实数a=( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
6.已知函数f(x)是定义在R上的奇函数,当x∈[-1,0)时,f(x)=x+3,则f($\frac{1}{2}$)=( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{7}{2}$ | C. | -$\frac{5}{2}$ | D. | -2 |
 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.