题目内容
2.定义在R上的函数f(x)满足f(x+6)=f(x).当x∈[-3,-1)时,f(x)=-(x+2)2,当x∈[-1,3)时,f(x)=x,则f(1)+f(2)+f(3)+…+f(2015)=( )| A. | 336 | B. | 355 | C. | 1676 | D. | 2015 |
分析 直接利用函数的周期性,求出函数在一个周期内的和,然后求解即可.
解答 解:定义在R上的函数f(x)满足f(x+6)=f(x).可得函数的周期为:6,
当x∈[-3,-1)时,f(x)=-(x+2)2,
当x∈[-1,3)时,f(x)=x,f(1)=1,f(2)=2,f(3)=f(-3)=-1,f(4)=f(-2)=0,f(5)=f(-1)=-1,f(6)=f(0)=0,
2015=6×335+5,
f(1)+f(2)+f(3)+…+f(2015)=f(1)+f(2)+f(3)+f(4)+f(5)+335[f(1)+f(2)+…+f(6)]=1+2-1+0-1+335×(1+2-1+0-1+0)=336.
故选:A.
点评 本题考查数列与函数相结合,函数的值的求法,函数的周期性的应用,考查计算能力.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
12.设点P在曲线y=x2+1(x≥0)上,点Q在曲线y=$\sqrt{x-1}$(x≥1)上,则|PQ|的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{3\sqrt{2}}{4}$ | C. | $\sqrt{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
10.已知圆锥曲线nx2+y2=1的离心率为2,则实数n的值为( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
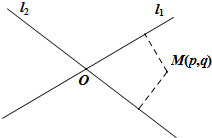 如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.
如图,平面中两条直线l1和l2相交于点O,对于平面上任意一点M,若p,q分别是M到直线l1和l2的距离,则称有序非负实数对(p,q)是点M的“距离坐标”.