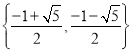题目内容
【题目】已知函数![]() ,
,![]() .
.
(I)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 存在极小值点
存在极小值点![]() ,且
,且![]() ,其中
,其中![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)试问过点![]() 可作多少条直线与
可作多少条直线与![]() 的图像相切?并说明理由.
的图像相切?并说明理由.
【答案】(Ⅰ)单调减区间为![]() 单调增区间为
单调增区间为![]() ;(Ⅱ)证明见解析;(Ⅲ)答案见解析.
;(Ⅱ)证明见解析;(Ⅲ)答案见解析.
【解析】分析:(1)对![]() 进行求导计算即可得到单调区间;
进行求导计算即可得到单调区间;
(2)若![]() 存在极小值点
存在极小值点![]() ,
,![]() ,则
,则![]() ,由
,由![]() 可得
可得![]() ,化简代入
,化简代入![]() ,即可得到证明;
,即可得到证明;
(2)设切点坐标是![]() ,依题意:
,依题意:![]() ,化简得:
,化简得:![]()
设![]() ,
,![]() ,故函数
,故函数![]() 在
在![]() 上零点个数,即是曲线切线的条数.
上零点个数,即是曲线切线的条数.![]() ,接下来对a进行分析讨论即可.
,接下来对a进行分析讨论即可.
解析:(1) ![]() ,
,![]()
所以![]() 的单调减区间为
的单调减区间为![]() 单调增区间为
单调增区间为![]() ;
;
(2) ![]() ,
,![]() 存在极小值点
存在极小值点![]() ,则
,则![]() .
.
![]() ,则
,则![]() ,
,
所以![]()
![]() 代入
代入![]() 所以
所以![]()
![]() ,
,
则![]() ,又
,又![]() ,所以
,所以![]() ;
;
(3) ![]() 时,有1条切线;
时,有1条切线;![]() 时,有2条切线.
时,有2条切线.
设切点坐标是![]() ,依题意:
,依题意:![]()
即![]() ,化简得:
,化简得:![]()
设![]() ,
,![]()
故函数![]() 在
在![]() 上零点个数,即是曲线切线的条数.
上零点个数,即是曲线切线的条数.
![]() ,
,
①当![]() 时,
时, ![]() ,在
,在![]() 上恰有一个零点1;
上恰有一个零点1;
②当![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,
,![]()
故![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
当![]() 时,
时, ![]() 在
在![]() 上恰有个零点;
上恰有个零点;
③![]() 时,
时,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
故![]() 在
在![]() 至多有两个零点,且
至多有两个零点,且![]()
又函数![]() 在
在![]() 单调递增,且值域是
单调递增,且值域是![]() ,
,
故对任意实数![]() ,必存在
,必存在![]() ,使
,使![]() ,此时
,此时
![]()
![]()
由于![]() ,
,
函数![]() 在
在![]() 上必有一零点;
上必有一零点;
![]()
![]()
![]()
先证明当![]() 时,
时, ![]() ,即证
,即证![]()
若![]() ,
,![]() ,而
,而![]() ,由于
,由于![]()
若![]() ,构建函数
,构建函数
![]()
![]() ,
,![]()
![]()
![]()
![]() 在
在![]() 为增函数,
为增函数, ![]()
![]()
综上![]() 时,
时,![]() ,所以
,所以
![]()
![]()
![]() ,故
,故![]()
又![]() ,
,![]() ,所以在
,所以在![]() 必有一零点.
必有一零点.
![]() 当
当![]() 时,
时, ![]() 在
在![]() 上有两个零点
上有两个零点
![]() 综上:
综上:![]() 时,有1条切线;
时,有1条切线;![]() 时,有2条切线.
时,有2条切线.

练习册系列答案
相关题目