题目内容
14.在由0,1,2,3,4,这5个数字组成数字不重复的五位数中,从小到大排列的第86个数是42031.分析 根据题意,将“由0,1,2,3,4,这5个数字组成数字不重复的五位数”按首位数字不同讨论可得:首位数字为1、2、3的五位数共有72个,4在首位,0在第二位的五位数有6个,4在首位,1在第二位的五位数有6个,此时在由0,1,2,3,4,这5个数字组成数字不重复的五位数中,从小到大排列排到了72+6+6=84个,继续列举第85个和第86个五位数,即可得答案.
解答 解:根据题意,用0,1,2,3,4,这5个数字组成数字不重复的五位数中,
1在首位时,将其他4个数字全排列,安排在剩余4个数位,有A44种情况,
则1在首位的五位数有A44=24个,
同理2在首位的五位数有A44=24个,
3在首位的五位数有A44=24个,
则首位是1、2、3的五位数有24×3=72个;
4在首位,0在第二位的五位数有A33=6个,
4在首位,1在第二位的五位数有A33=6个,
此时在由0,1,2,3,4,这5个数字组成数字不重复的五位数中,从小到大排列排到了72+6+6=84个,
第85个数为42013,第86个数为42031,
故答案为:42031.
点评 本题考查排列、组合的应用,解题的关键是结合实数大小运用排列、组合的知识将“0,1,2,3,4,这5个数字组成数字不重复的五位数”进行分类讨论.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
20.某中学四名高二学生约定“五一”节到本地区三处旅游景点做公益活动,如果每个景点至少一名同学,且甲乙两名同学不在同一景点,则这四名同学的安排情况有( )
| A. | 10种 | B. | 20种 | C. | 30种 | D. | 40种 |
5.按如下程序框图,若输出结果为170,则在判断框内应补充的条件为( )
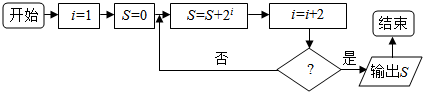

| A. | i≥7 | B. | i>9 | C. | i≥9 | D. | i>10 |
2.计算tan20°+$\frac{2sin40°}{cos20°}$的值为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 2 |
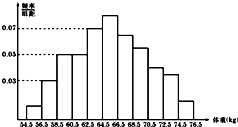 为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.
为了了解某市高三学生的身体发育情况,抽测了该市50名高三男生的体重(kg),数据得到的频率分布直方图如图.根据右图可知这50名男生中体重在[56.5,60.5]的人数是8.