题目内容
4.已知函数f(x)=|x-a|+|x+1|(Ⅰ)当a=1时,解不等式f(x)<3;
(Ⅱ)若f(x)的最小值为1,求a的值.
分析 (Ⅰ)当a=1时,利用绝对值的意义求得不等式f(x)<3的解集.
(Ⅱ)由条件利用绝对值的意义可得f(x)的最小值为|a+1|=1,由此求得a的值.
解答 解:(Ⅰ)当a=1时,f(x)=|x-1|+|x+1|表示数轴上的x对应点到1、-1对应点的距离之和,
而-$\frac{3}{2}$和$\frac{3}{2}$对应点到1、-1对应点的距离之和正好等于3,故不等式f(x)<3的解集为{x|-$\frac{3}{2}$<x<$\frac{3}{2}$}.
(Ⅱ)函数f(x)=|x-a|+|x+1|表示数轴上的x对应点到a、-1对应点的距离之和,它的最小值为|a+1|=1,
可得a=0,或a=-2.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,属于基础题.

练习册系列答案
相关题目
9.$\int_0^1{({e^x}+2x)dx=}$( )
| A. | 1 | B. | e-1 | C. | e | D. | e+1 |
 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.
为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.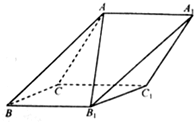 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.