题目内容
在边长为1的正方形ABCD中,E为AB的中点,P为以A为圆心,AB为半径的圆在正方形内的圆弧上的任意一点,设向量
=λ
+μ
.
(Ⅰ)求点(μ,λ)的轨迹方程(不需限制变量取值范围);
(Ⅱ)求λ+μ的最小值.
| AC |
| DE |
| AP |
(Ⅰ)求点(μ,λ)的轨迹方程(不需限制变量取值范围);
(Ⅱ)求λ+μ的最小值.
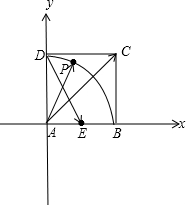
(Ⅰ)如图,
以A为原点,以AB所在的为x轴,建立坐标系,设正方形ABCD的边长为1,
设E(
,0),C(1,1),D(0,1),A(0,0).
设P(cosθ,sinθ),∴
=(1,1).
由向量
=λ
+μ
=λ(
,-1)+μ(cosθ,sinθ)
=(
+μcosθ,-λ+μsinθ)=(1,1),
∴
+μcosθ=1,-λ+μsinθ=1,
即μcosθ=1-
①,
μsinθ=1+λ ②.
①2+②2得:5λ2+4λ-4μ2+8=0;
(Ⅱ)由
+μcosθ=1,-λ+μsinθ=1,
∴
,
∴λ+μ=
,
由题意可知:0≤θ≤
,∴0≤sinθ≤1,0≤cosθ≤1,
∴当cosθ取得最大值1时,同时sinθ取得最小值0,这时λ+μ取最小值为
=
.
∴λ+μ的最小值为
.
以A为原点,以AB所在的为x轴,建立坐标系,设正方形ABCD的边长为1,
设E(
| 1 |
| 2 |
设P(cosθ,sinθ),∴
| AC |
由向量
| AC |
| DE |
| AP |
=λ(
| 1 |
| 2 |
=(
| λ |
| 2 |
∴
| λ |
| 2 |
即μcosθ=1-
| λ |
| 2 |
μsinθ=1+λ ②.
①2+②2得:5λ2+4λ-4μ2+8=0;
(Ⅱ)由
| λ |
| 2 |
∴
|
∴λ+μ=
| 2sinθ-2cosθ+3 |
| sinθ+2cosθ |
由题意可知:0≤θ≤
| π |
| 2 |
∴当cosθ取得最大值1时,同时sinθ取得最小值0,这时λ+μ取最小值为
| 0-2+3 |
| 0+2 |
| 1 |
| 2 |
∴λ+μ的最小值为
| 1 |
| 2 |


练习册系列答案
相关题目










 )
) ;(2)求
;(2)求 的取值范围
的取值范围



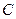 的极坐标方程为
的极坐标方程为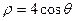 ,直线
,直线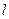 的参数方程是:
的参数方程是:
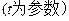 .
.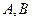 两点,求
两点,求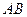 长.
长.