题目内容
已知圆x2+y2=9,从这个圆上任一点P向x轴作垂线PP′,点P′为垂足,点M在PP′上,并且
=
.
(1)求点M的轨迹.
(2)若F1(-
,0),F2(
,0)求|MF1||MF2|的最大值.
| PM |
| 1 |
| 2 |
| MP′ |
(1)求点M的轨迹.
(2)若F1(-
| 5 |
| 5 |
(1)根据题意,设P(m,n),
则P'(m,0),
设M(x,y),由
=
可得
,即
将P(x,
y)代入x2+y2=9,可得x2+(
y)2=9,
化简得
+
=1,即为点M的轨迹方程.
(2)由(1)得M的轨迹方程
+
=1,c=
=
.
∴点M的轨迹是以F1(-
,0),F2(
,0)为焦点的椭圆.
根据椭圆的定义,可得|MF1|+|MF2|2a=6,
∴|MF1||MF2|≤(
)2=9,
当且仅当|MF1|=|MF2|=3时,|MF1||MF2|的最大值为9.
则P'(m,0),
设M(x,y),由
| PM |
| 1 |
| 2 |
| MP′ |
|
|
将P(x,
| 3 |
| 2 |
| 3 |
| 2 |
化简得
| x2 |
| 9 |
| y2 |
| 4 |
(2)由(1)得M的轨迹方程
| x2 |
| 9 |
| y2 |
| 4 |
| a2-b2 |
| 5 |
∴点M的轨迹是以F1(-
| 5 |
| 5 |
根据椭圆的定义,可得|MF1|+|MF2|2a=6,
∴|MF1||MF2|≤(
| |MF1|+|MF2| |
| 2 |
当且仅当|MF1|=|MF2|=3时,|MF1||MF2|的最大值为9.

练习册系列答案
相关题目
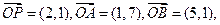 设
设 是直线
是直线 上的一点, (其中
上的一点, (其中 为坐标原点).
为坐标原点).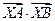 取最小值时的点
取最小值时的点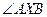 的余弦值.
的余弦值. 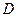 是线段
是线段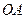 的三等分点,且
的三等分点,且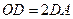 ,
,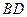 与
与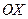 交于点
交于点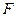 ,设
,设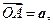
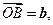 试用
试用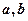 表示
表示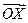 和
和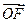 .
. 
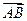 的坐标.
的坐标.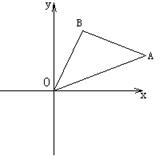
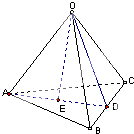
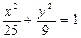 上一点,
上一点, 、
、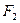 为左右焦点,若
为左右焦点,若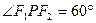
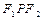 的面积;
的面积;