题目内容
14.已知F1,F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>$\sqrt{3}$)的两个焦点,P为椭圆上一点,且△PF1F2是直角三角形,且S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{3}{2}$,则a=2.分析 分类讨论,利用S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{3}{2}$,得到a.
解答 解:由题意,c=$\sqrt{{a}^{2}-3}$,
①若PF1⊥x轴时,取P(-c,$\frac{3}{a}$),S${\;}_{△P{F}_{1}{F}_{2}}$=$\frac{1}{2}•2\sqrt{{a}^{2}-3}•\frac{3}{a}$=$\frac{3}{2}$,∴a=2
同理,PF2⊥x轴时,a=2;
②∠F1PF2=90°,设|PF1|=t1,|PF2|=t2,
则t1+t2=2a①,t12+t22=4a2-12②,
由①2-②得t1t2=12,S${\;}_{△P{F}_{1}{F}_{2}}$=6,不符合题意.
故答案为:2.
点评 本题主要考查了椭圆的标准方程、椭圆的简单性质.解答的关键是通过勾股定理解三角形,考查计算能力.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
4.设$\overrightarrow{a}$,$\overrightarrow{b}$是非零向量,k∈R,则$\overrightarrow{a}$=k$\overrightarrow{b}$是$\overrightarrow{a}$与$\overrightarrow{b}$平行的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分非必要条件 |
5.已知P,A,B,C是平面内四点,且$\overrightarrow{PA}$+$\overrightarrow{PB}$+$\overrightarrow{PC}$=$\overrightarrow{AC}$,则以下一定共线的是( )
| A. | $\overrightarrow{PC}$与$\overrightarrow{PB}$ | B. | $\overrightarrow{PA}$与$\overrightarrow{PB}$ | C. | $\overrightarrow{PA}$与$\overrightarrow{PC}$ | D. | $\overrightarrow{PC}$与$\overrightarrow{AB}$ |
19.在直角三角形ABC中,C=90°,B=30°,AB=4,M是AB的中点,将三角形ACM沿CM翻折成直二面角,则三棱锥A-CBM的外接球的表面积为( )
| A. | $\frac{52π}{3}$ | B. | $\frac{18π}{5}$ | C. | $\frac{14π}{3}$ | D. | 12π |
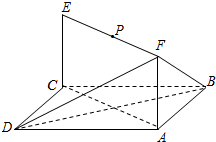 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2},AF=1$.P为线段EF上一点.
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,$AB=\sqrt{2},AF=1$.P为线段EF上一点.