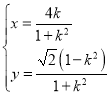题目内容
【题目】三棱锥![]() 中,顶点
中,顶点![]() 在底面
在底面![]() 的投影为
的投影为![]() 的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥
的内心,三个侧面的面积分别为12,16,20,且底面面积为24,则三棱锥![]() 的内切球的表面积为( )
的内切球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
若设![]() 在底面
在底面![]() 的投影为
的投影为![]() ,分别作
,分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则
,则![]()
![]()
![]() .依题意,
.依题意,![]() 为
为![]() 的内心,则
的内心,则![]() ,故
,故![]() ,再利用三个侧面的面积分别为12,16,20,可得
,再利用三个侧面的面积分别为12,16,20,可得![]() ,从而求出
,从而求出![]() ,然后求
,然后求![]() 内切圆半径,再求出三棱锥的体积,再用
内切圆半径,再求出三棱锥的体积,再用![]() ,可求出内切球的半径,从而可求出内切球的表面积.
,可求出内切球的半径,从而可求出内切球的表面积.
解法一:不妨设![]()
设![]() 在底面
在底面![]() 的投影为
的投影为![]() ,分别作
,分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则
,则![]()
![]()
![]() .依题意,
.依题意,![]() 为
为![]() 的内心,则
的内心,则![]() ,故
,故![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() .
.
令![]() .
.
所以![]() ,解得
,解得![]() ,所以
,所以![]() .
.
设![]() 内切圆半径为
内切圆半径为![]() ,则
,则![]() ,即
,即![]() ,解得
,解得![]() ,故
,故![]() .
.
由![]() ,得
,得![]() ,
,
所以![]() ,
,
所以![]() ,
,
设三棱锥![]() 的内切球的半径为
的内切球的半径为![]() ,则
,则
![]() ,即
,即![]() ,解得
,解得![]() ,所以三棱锥
,所以三棱锥![]() 的内切球的表面积为
的内切球的表面积为![]() ,故选C.
,故选C.
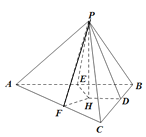
解法二:不妨设![]()
设![]() 在底面
在底面![]() 的投影为
的投影为![]() ,分别作
,分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,则
,则![]()
![]()
![]() .依题意,
.依题意,![]() 为
为![]() 的内心,则
的内心,则![]() ,
,
故![]() ,且
,且![]() ,记为
,记为![]() .
.
所以![]() ,故
,故![]() ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,
,
![]() ,
,
所以![]() ,所以
,所以![]() .
.
令![]() .
.
所以![]() ,解得
,解得![]() ,所以
,所以![]() .
.
设![]() 内切圆半径为
内切圆半径为![]() ,由直角三角形内切圆半径公式得
,由直角三角形内切圆半径公式得![]() .
.
由题意知三棱锥内切球的球心在![]() 上,设为点
上,设为点![]() .由条件知点
.由条件知点![]() 也在
也在![]() 的角平分线上,所以内切球半径
的角平分线上,所以内切球半径![]() ,所以三棱锥
,所以三棱锥![]() 的内切球的表面积为
的内切球的表面积为![]() ,
,
故选:C

【题目】某省![]() 年开始将全面实施新高考方案.在
年开始将全面实施新高考方案.在![]() 门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为
门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共
共![]() 个等级,各等级人数所占比例分别为
个等级,各等级人数所占比例分别为![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() ,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
(1)某校生物学科获得![]() 等级的共有10名学生,其原始分及转换分如下表:
等级的共有10名学生,其原始分及转换分如下表:
原始分 | 91 | 90 | 89 | 88 | 87 | 85 | 83 | 82 |
转换分 | 100 | 99 | 97 | 95 | 94 | 91 | 88 | 86 |
人数 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 1 |
现从这10名学生中随机抽取3人,设这3人中生物转换分不低于![]() 分的人数为
分的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)假设该省此次高一学生生物学科原始分![]() 服从正态分布
服从正态分布![]() .若
.若![]() ,令
,令![]() ,则
,则![]() ,请解决下列问题:
,请解决下列问题:
①若以此次高一学生生物学科原始分![]() 等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
②现随机抽取了该省![]() 名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记
名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记![]() 为被抽到的原始分不低于
为被抽到的原始分不低于![]() 分的学生人数,求
分的学生人数,求![]() 取得最大值时
取得最大值时![]() 的值.
的值.
附:若![]() ,则
,则![]() ,
,![]() .
.
【题目】正态分布有极其广泛的实际背景,生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述.例如,同一种生物体的身长、体重等指标.随着“绿水青山就是金山银山”的观念不断的深入人心,环保工作快速推进,很多地方的环境出现了可喜的变化.为了调查某水库的环境保护情况,在水库中随机捕捞了100条鱼称重.经整理分析后发现,鱼的重量x(单位:kg)近似服从正态分布![]() ,如图所示,已知
,如图所示,已知![]() .
.
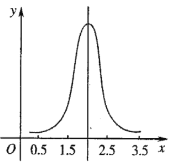
(Ⅰ)若从水库中随机捕捞一条鱼,求鱼的重量在![]() 内的概率;
内的概率;
(Ⅱ)(ⅰ)从捕捞的100条鱼中随机挑出6条鱼测量体重,6条鱼的重量情况如表.
重量范围(单位:kg) |
|
|
|
条数 | 1 | 3 | 2 |
为了进一步了解鱼的生理指标情况,从6条鱼中随机选出3条,记随机选出的3条鱼中体重在![]() 内的条数为X,求随机变量X的分布列和数学期望;
内的条数为X,求随机变量X的分布列和数学期望;
(ⅱ)若将选剩下的94条鱼称重做标记后立即放生.两周后又随机捕捞1000条鱼,发现其中带有标记的有2条.为了调整生态结构,促进种群的优化,预备捕捞体重在![]() 内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在
内的鱼的总数的40%进行出售,试估算水库中鱼的条数以及应捕捞体重在![]() 内的鱼的条数.
内的鱼的条数.