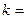题目内容
若直线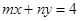 与圆
与圆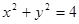 没有交点,则过点
没有交点,则过点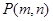 的直线与椭圆
的直线与椭圆 的公共点个数为( )
的公共点个数为( )
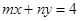 与圆
与圆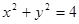 没有交点,则过点
没有交点,则过点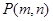 的直线与椭圆
的直线与椭圆 的公共点个数为( )
的公共点个数为( )| A.至少一个 | B.0个 | C.1个 | D.2个 |
D
分析:先根据题意可知原点到直线mx+ny-4=0的距离大于等于 2求得m和n的范围可推断点P(m,n)是以原点为圆心,2为半径的圆内的点,根据圆的方程和椭圆方程可知圆x2+y2=4内切于椭圆,进而可知点P是椭圆内的点,进而判断可得答案.
解:因为直线mx+ny=4和圆x2+y2=4没有公共点,
所以原点到直线mx+ny-4=0的距离d= >2,
>2,
所以m2+n2<4,
所以点P(m,n)是在以原点为圆心,2为半径的圆内的点.
∵椭圆的长半轴 3,短半轴为 2
∴圆x2+y2=4内切于椭圆
∴点P是椭圆内的点
∴过点P(m,n)的一条直线与椭圆的公共点数为2.
故选D.
点评:本题主要考查了直线与圆、直线与圆锥曲线的关系,以及点到直线的距离公式,解决此类问题可采用数形结合的方法较为直观.
解:因为直线mx+ny=4和圆x2+y2=4没有公共点,
所以原点到直线mx+ny-4=0的距离d=
 >2,
>2,所以m2+n2<4,
所以点P(m,n)是在以原点为圆心,2为半径的圆内的点.
∵椭圆的长半轴 3,短半轴为 2
∴圆x2+y2=4内切于椭圆
∴点P是椭圆内的点
∴过点P(m,n)的一条直线与椭圆的公共点数为2.
故选D.
点评:本题主要考查了直线与圆、直线与圆锥曲线的关系,以及点到直线的距离公式,解决此类问题可采用数形结合的方法较为直观.

练习册系列答案
相关题目
(本题15分)已知曲线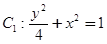 与曲线
与曲线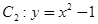 ,设点
,设点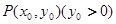 是曲线
是曲线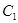 上任意一点,直线
上任意一点,直线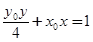 与曲线
与曲线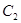 交于
交于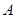 、
、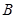 两点.
两点.
(1)判断直线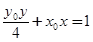 与曲线
与曲线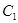 的位置关系;
的位置关系;
(2)以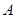 、
、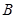 两点为切点分别作曲线
两点为切点分别作曲线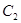 的切线,设两切线的交点为
的切线,设两切线的交点为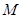 ,求证:点
,求证:点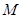 到直线
到直线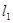 :
: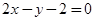 与
与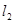 :
: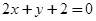 距离的乘积为定值.
距离的乘积为定值.
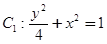 与曲线
与曲线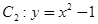 ,设点
,设点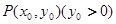 是曲线
是曲线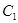 上任意一点,直线
上任意一点,直线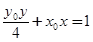 与曲线
与曲线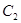 交于
交于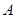 、
、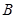 两点.
两点.(1)判断直线
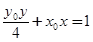 与曲线
与曲线 的位置关系;
的位置关系;(2)以
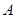 、
、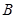 两点为切点分别作曲线
两点为切点分别作曲线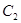 的切线,设两切线的交点为
的切线,设两切线的交点为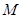 ,求证:点
,求证:点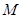 到直线
到直线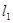 :
: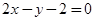 与
与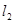 :
: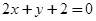 距离的乘积为定值.
距离的乘积为定值. =1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2
=1(a>b>0)的左、右焦点,过F2的直线l与椭圆C相交于A,B两点,直线l的倾斜角为60°,F1到直线l的距离为2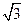 .
.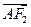 =2
=2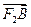 ,求椭圆C的方程.
,求椭圆C的方程.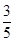 或
或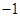
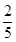
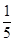 或
或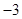
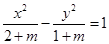 表示双曲线”的一个充分不必要条件是( )
表示双曲线”的一个充分不必要条件是( )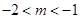
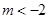 或
或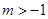
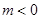
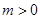
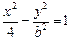
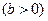 的渐近线方程式为
的渐近线方程式为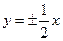 ,则
,则 等于
等于 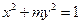 的焦点在
的焦点在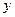 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则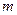 的值为________
的值为________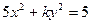 的一个焦点是
的一个焦点是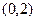 ,那么
,那么