题目内容
某厂生产某种产品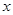 (百台),总成本为
(百台),总成本为 (万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入
(万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入 (万元),假定该产品产销平衡。
(万元),假定该产品产销平衡。
(1)若要该厂不亏本,产量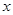 应控制在什么范围内?
应控制在什么范围内?
(2)该厂年产多少台时,可使利润最大?
(3)求该厂利润最大时产品的售价。
(1) ;(2)当年产
;(2)当年产 台时,可使利润最大;(3)
台时,可使利润最大;(3) 元/台.
元/台.
解析试题分析:(1)该厂不亏本即 ;(2)利润最大即
;(2)利润最大即 的最大值,因是分段函数,需求得每段的最大值,然后最大的所求;(3)有
的最大值,因是分段函数,需求得每段的最大值,然后最大的所求;(3)有 可得产品的售价.
可得产品的售价.
试题解析:由题意得,成本函数为 ,从而利润函数
,从而利润函数 。 2分
。 2分
(1)要使不亏本,只要 ,
,
当 时,
时, , 4分
, 4分
当 时,
时, ,
,
综上,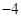 , 6分
, 6分
答:若要该厂不亏本,产量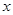 应控制在100台到550台之间。 7分
应控制在100台到550台之间。 7分
(2)当 时,
时, ,
,
故当 时,
时, (万元) 9分
(万元) 9分
当 时,
时, , 10分
, 10分
综上,当年产300台时,可使利润最大。 11分
(3)由(2)知 ,时,利润最大,此时的售价为
,时,利润最大,此时的售价为 (万元/百台)=233元/台。 14分
(万元/百台)=233元/台。 14分
考点:1.函数的应用;2.解一元二次不等式和求一元二次函数最值.

练习册系列答案
相关题目
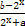 是奇函数.
是奇函数. ,函数
,函数 .
.
 时,画出函数
时,画出函数 的大致图像;
的大致图像; 解的个数.
解的个数. 满足
满足 ,且
,且 .
. 时,函数
时,函数 的图像恒在函数
的图像恒在函数 的图像的上方,求实数
的图像的上方,求实数 的取值范围.
的取值范围. 过点
过点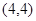 .
. ;
; 的图像向下平移1个单位,再向右平移
的图像向下平移1个单位,再向右平移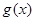 图像,设函数
图像,设函数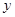 轴对称的函数为
轴对称的函数为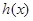 ,试求
,试求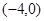 上的函数
上的函数 ,若在其定义域内,不等式
,若在其定义域内,不等式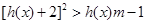 恒成立,求实数
恒成立,求实数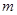 的取值范围.
的取值范围. 的定义域为
的定义域为 ,且
,且 (
( 且
且 ),存在
),存在 ,使得
,使得 ,则称
,则称 .
. ,
, ,判断
,判断 ,并说明理由;
,并说明理由; 若
若 ,
, 且
且 ,函数
,函数 .
. .
.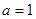 时,函数
时,函数 的图像在点
的图像在点 处的切线方程;
处的切线方程; 时,解不等式
时,解不等式 ;
;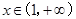 ,直线
,直线 的图像下方.求整数
的图像下方.求整数 的最大值.
的最大值. .
. 在
在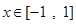 上的最大值和最小值;
上的最大值和最小值; 的值域。(用a表示)
的值域。(用a表示) 是定义域为
是定义域为 的单调减函数,且是奇函数,当
的单调减函数,且是奇函数,当 时,
时,
 的不等式
的不等式