题目内容
已知函数 .
.
(Ⅰ)当a=3时,求函数 在
在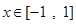 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)求函数 的定义域,并求函数
的定义域,并求函数 的值域。(用a表示)
的值域。(用a表示)
(Ⅰ)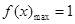 ,
,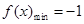 ;(Ⅱ)
;(Ⅱ) 的定义域为
的定义域为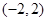 ,
, 的值域为
的值域为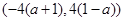 .
.
解析试题分析:(Ⅰ)当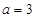 时,求函数
时,求函数 在
在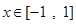 上的最大值和最小值,令
上的最大值和最小值,令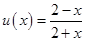 ,变形得到该函数的单调性,求出其值域,再由
,变形得到该函数的单调性,求出其值域,再由 为增函数,从而求得函数
为增函数,从而求得函数 在
在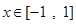 上的最大值和最小值;(Ⅱ)求函数
上的最大值和最小值;(Ⅱ)求函数 的定义域,由对数函数的真数大于0求出函数
的定义域,由对数函数的真数大于0求出函数 的定义域,求函数
的定义域,求函数 的值域,函数
的值域,函数 的定义域,即
的定义域,即 的定义域,把
的定义域,把 的解析式代入
的解析式代入 后整理,化为关于
后整理,化为关于 的二次函数,对
的二次函数,对 分类讨论,由二次函数的单调性求最值,从而得函数
分类讨论,由二次函数的单调性求最值,从而得函数 的值域.
的值域.
试题解析:(Ⅰ)令 ,显然
,显然 在
在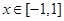 上单调递减,故
上单调递减,故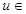
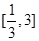 ,
,
故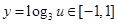 ,即当
,即当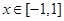 时,
时,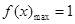 ,(在
,(在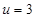 即
即 时取得)
时取得)
??????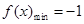 ,(在
,(在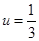 即
即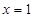 时取得)
时取得)
(II)由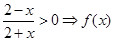 的定义域为
的定义域为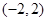 ,由题易得:
,由题易得: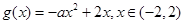 ,
,
因为 ,故
,故 的开口向下,且对称轴
的开口向下,且对称轴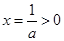 ,于是:
,于是: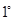 ?当
?当 即
即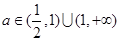 时,
时, 的值域为(
的值域为(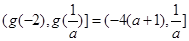 ;
; ?当
?当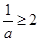 即
即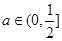 时,
时, 的值域为(
的值域为(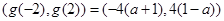
考点:复合函数的单调性;函数的值域.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
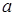 为正实数,函数
为正实数,函数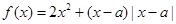 .
.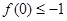 ,求
,求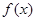 的最小值;
的最小值;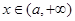 ,求不等式
,求不等式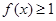 的解集.
的解集.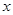 (百台),总成本为
(百台),总成本为 (万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入
(万元),其中固定成本为2万元, 每生产1百台,成本增加1万元,销售收入 (万元),假定该产品产销平衡。
(万元),假定该产品产销平衡。 的图象经过点
的图象经过点 .
. 上的单调性,并用单调性的定义证明.
上的单调性,并用单调性的定义证明.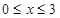 时,f(x)=
时,f(x)=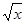 -1.
-1.
 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围. 在
在 上是减函数,且为奇函数,满足
上是减函数,且为奇函数,满足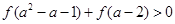 ,试
,试 求的范围.
求的范围. 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有 (
( ,
, )成立,则称
)成立,则称 阶缩放函数.
阶缩放函数. 时,
时, ,求
,求 的值;
的值; ,求证:函数
,求证:函数 在
在 上无零点;
上无零点; 时,
时, ,求
,求 (
( )上的取值范围.
)上的取值范围. 满足
满足 ,且
,且 。
。 的奇偶性并证明之;
的奇偶性并证明之; 的不等式:
的不等式: ;
; ,
, .
. ,若集合
,若集合 有且仅有一个元素,求证:
有且仅有一个元素,求证:  。
。