题目内容
【题目】曲线C是平面内与两个定点
，
的距离之积等于常数
的点的轨迹，给出下列三个结论：
①曲线过坐标原点；②曲线关于坐标原点对称；
③曲线关于横轴对称；④曲线关于纵轴对称；
⑤曲线关于
对称；⑥若点P在曲线上，则
的面积不大于
.
其中，所有正确结论的序号是______．
【答案】②③④⑥
【解析】
首先确定点
的轨迹方程；将
代入方程可知方程不成立，①错误；将
、
、
和
依次代入曲线方程，验证方程是否成立，可确定②③④⑤的真假；利用
可知⑥正确.
设
，则
当
，
时，
，曲线不过坐标原点，①错误；
若
在曲线上，将代入曲线方程可知方程成立，则曲线关于原点对称，②正确；
若在曲线上，将代入曲线方程可知方程成立，则曲线关于横轴对称，③正确；
若在曲线上，将代入曲线方程可知方程成立，则曲线关于纵轴对称，④正确；
若在曲线上，将代入曲线方程可知方程不成立，则曲线不关于
对称，⑤错误；
，⑥正确.
故答案为：②③④⑥
【题目】团体购买公园门票，票价如下表：
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园，若按部门作为团体，选择两个不同的时间分别购票游览公园，则共需支付门票费为1290元；若两个部门合在一起作为一个团体，同一时间购票游览公园，则需支付门票费为990元，那么这两个部门的人数之差为( )
A. 
B. 
C. 
D. 
【题目】某城市的公交公司为了方便市民出行，科学规划车辆投放，在一个人员密集流动地段增设一个起点站，为了研究车辆发车间隔时间
与乘客等候人数
之间的关系，经过调查得到如下数据：
间隔时间（ | 10 | 11 | 12 | 13 | 14 | 15 |
等候人数（ | 23 | 25 | 26 | 29 | 28 | 31 |
调查小组先从这6组数据中选取4组数据求线性回归方程，再用剩下的2组数据进行检验.检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数
，再求与实际等候人数的差，若差值的绝对值不超过1，则称所求方程是“恰当回归方程”.
（1）若选取的是后面4组数据，求关于的线性回归方程
；
（2）判断（1）中的方程是否是“恰当回归方程”；
（3）为了使等候的乘客不超过35人，试用（1）中方程估计间隔时间最多可以设置为多少（精确到整数）分钟？
附：对于一组数据
，
，…，
，其回归直线的斜率和截距的最小二乘估计分别为：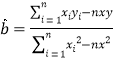
，
.
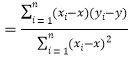