题目内容
1.已知函数f(x)=x+$\frac{a}{x}$-2,若x∈[2,+∞)恒有f(x)>1,求a的取值范围.分析 由参数分离可得a>x(3-x)在x≥2恒成立,由二次函数的最值求法,可得y=x(3-x)的最大值,再由恒成立思想可得a的范围.
解答 解:f(x)>1,即为
a>x(3-x)在x≥2时恒成立,
由y=x(3-x)=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
区间[2,+∞)为减区间,
即有x=2时,取得最大值2.
则有a>2.
即有a的取值范围是(2,+∞).
点评 本题考查函数恒成立问题的解法,注意运用参数分离和二次函数的最值的求法,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.某算法程序如图所示,执行该程序,若输入4,则输出的S为( )
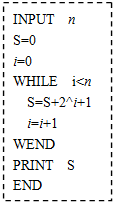
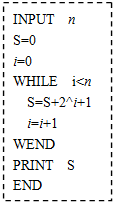
| A. | 36 | B. | 19 | C. | 16 | D. | 10 |
13.若函数f(x)=x+$\frac{b}{x}$(b∈R)的导函数在区间(2,4)上有零点,则f(x)在下列区间单调递增的是( )
| A. | (2,+∞) | B. | (-∞,-3) | C. | ($\sqrt{2}$,2) | D. | (-8,-4) |
10.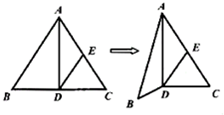 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 0 |
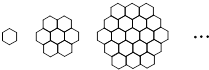 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看做是一各正六边形,如图为一组蜂巢的截面图,其中第一图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看做是一各正六边形,如图为一组蜂巢的截面图,其中第一图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.