题目内容
已知F1,F2是椭圆C: +
+ =1(a>b>0)的左、右焦点,点P(-
=1(a>b>0)的左、右焦点,点P(- ,1)在椭圆上,线段PF2与y轴的交点M满足
,1)在椭圆上,线段PF2与y轴的交点M满足 +
+ =0.
=0.
(1)求椭圆C的方程;
(2)椭圆C上任一动点N(x0,y0)关于直线y=2x的对称点为N1(x1,y1),求3x1-4y1的取值范围.
 +
+ =1(a>b>0)的左、右焦点,点P(-
=1(a>b>0)的左、右焦点,点P(- ,1)在椭圆上,线段PF2与y轴的交点M满足
,1)在椭圆上,线段PF2与y轴的交点M满足 +
+ =0.
=0.(1)求椭圆C的方程;
(2)椭圆C上任一动点N(x0,y0)关于直线y=2x的对称点为N1(x1,y1),求3x1-4y1的取值范围.
(1) +
+ =1 (2)[-10,10]
=1 (2)[-10,10]
 +
+ =1 (2)[-10,10]
=1 (2)[-10,10](1)点P(- ,1)在椭圆上,
,1)在椭圆上,
∴ +
+ =1.①
=1.①
又∵ +
+ =0,M在y轴上,
=0,M在y轴上,
∴M为PF2的中点,
∴- +c=0,c=
+c=0,c= .
.
∴a2-b2=2,②
联立①②,解得b2=2(b2=-1舍去),
∴a2=4.
故所求椭圆C的方程为 +
+ =1.
=1.
(2)∵点N(x0,y0)关于直线y=2x的对称点为N1(x1,y1),
∴
解得
∴3x1-4y1=-5x0.
∵点N(x0,y0)在椭圆C: +
+ =1上,
=1上,
∴-2≤x0≤2,
∴-10≤-5x0≤10,
即3x1-4y1的取值范围为[-10,10].
 ,1)在椭圆上,
,1)在椭圆上,∴
 +
+ =1.①
=1.①又∵
 +
+ =0,M在y轴上,
=0,M在y轴上,∴M为PF2的中点,
∴-
 +c=0,c=
+c=0,c= .
.∴a2-b2=2,②
联立①②,解得b2=2(b2=-1舍去),
∴a2=4.
故所求椭圆C的方程为
 +
+ =1.
=1.(2)∵点N(x0,y0)关于直线y=2x的对称点为N1(x1,y1),
∴

解得

∴3x1-4y1=-5x0.
∵点N(x0,y0)在椭圆C:
 +
+ =1上,
=1上,∴-2≤x0≤2,
∴-10≤-5x0≤10,
即3x1-4y1的取值范围为[-10,10].

练习册系列答案
相关题目
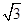 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.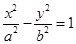
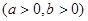 的渐近线方程为
的渐近线方程为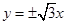 ,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )
,则以它的顶点为焦点,焦点为顶点的椭圆的离心率等于( )


 -
- =1
=1 -
- =1
=1 +
+ =1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=________.
=1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=________. 的离心率是
的离心率是 ,则
,则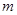 的值为 .
的值为 .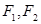 分别是椭圆
分别是椭圆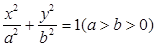 的左右焦点,
的左右焦点,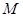 是
是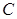 上一点且
上一点且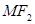 与
与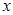 轴垂直,直线
轴垂直,直线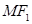 与
与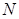 .
.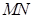 的斜率为
的斜率为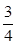 ,求
,求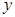 轴上的截距为
轴上的截距为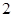 ,且
,且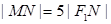 ,求
,求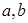 .
.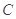 过点
过点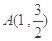 ,两个焦点为
,两个焦点为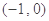 ,
,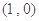 .
.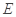 ,
,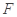 是椭圆
是椭圆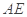 的斜率与
的斜率与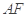 的斜率互为相反数,证明直线
的斜率互为相反数,证明直线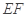 的斜率为定值,并求出这个定值.
的斜率为定值,并求出这个定值.