题目内容
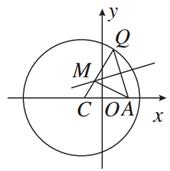
设圆(x+1)2+y2=25的圆心为C,A(1,0)是圆内一定点,Q为圆周上任一点.线段AQ的垂直平分线与CQ的连线交于点M,则M的轨迹方程为( )
A. - - =1 =1 | B. + + =1 =1 |
C. - - =1 =1 | D. + + =1 =1 |
D
M为AQ垂直平分线上一点,则|AM|=|MQ|,∴|MC|+|MA|=|MC|+|MQ|=|CQ|=5,故M的轨迹为椭圆,
∴a=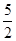 ,c=1,则b2=a2-c2=
,c=1,则b2=a2-c2=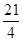 ,∴椭圆的标准方程为
,∴椭圆的标准方程为 +
+ =1.
=1.

∴a=
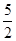 ,c=1,则b2=a2-c2=
,c=1,则b2=a2-c2=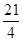 ,∴椭圆的标准方程为
,∴椭圆的标准方程为 +
+ =1.
=1.
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 ,
, 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 ,
, 两点,若
两点,若 ,
, ,则椭圆的离心率为( )
,则椭圆的离心率为( )
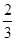


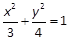 的左右两个顶点, P是该椭圆上异于A,B的任一点,则
的左右两个顶点, P是该椭圆上异于A,B的任一点,则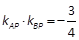 .
.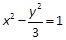 的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则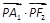 的最小值为-2.
的最小值为-2.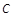 :
: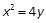 的焦点为
的焦点为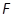 ,抛物线上一点
,抛物线上一点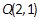 和抛物线内一点
和抛物线内一点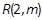
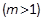 ,过点Q作抛物线的切线
,过点Q作抛物线的切线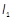 ,直线
,直线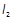 过点
过点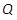 且与
且与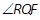 ;
;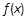 是定义在R上的奇函数,
是定义在R上的奇函数,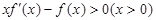 , 则不等式
, 则不等式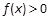 的解集是
的解集是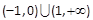 .
. +
+ =1(a>b>0)的左、右焦点,点P(-
=1(a>b>0)的左、右焦点,点P(- ,1)在椭圆上,线段PF2与y轴的交点M满足
,1)在椭圆上,线段PF2与y轴的交点M满足 +
+ =0.
=0. +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( ) )
)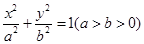 的左右焦点为F1,F2离心率为
的左右焦点为F1,F2离心率为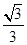 ,过F2的直线l交C与A,B两点,若△AF1B的周长为
,过F2的直线l交C与A,B两点,若△AF1B的周长为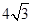 ,则C的方程为( )
,则C的方程为( )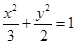
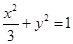


 过点
过点 且离心率为
且离心率为 .
. 的方程;
的方程; 的直线
的直线 交
交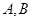 两点,且
两点,且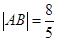 ,求直线
,求直线