题目内容
【题目】已知椭圆![]() 的对称轴为坐标轴,离心率为
的对称轴为坐标轴,离心率为![]() ,且一个焦点坐标为
,且一个焦点坐标为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,以线段
两点,以线段![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,其中点
,其中点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 为坐标原点,求点
为坐标原点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:
(1)由题意可求得![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)首先讨论斜率存在的情况,点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.
当斜率不存在时额外讨论可得结论.
试题解析:
解:(1)由已知设椭圆![]() 的方程为
的方程为![]() ,则
,则![]() .
.
由![]() ,得
,得![]() ,
, ![]() ,
, ![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.
(2)当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
则由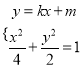 消去
消去![]() 得
得![]() .
.
![]() .①
.①
设点![]() ,
, ![]() ,
, ![]() 的坐标分别是
的坐标分别是![]() ,
, ![]() ,
, ![]() .
.
∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
![]() ,
,
由于点![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,
,
从而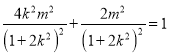 ,化简得
,化简得![]() ,经检验满足①式.
,经检验满足①式.
又点![]() 到直线
到直线![]() 的距离为
的距离为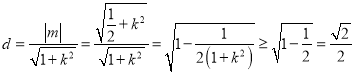 .
.
当且仅当![]() 时,等号成立.
时,等号成立.
当直线![]() 斜率不存在时,由对称性知,点
斜率不存在时,由对称性知,点![]() 一定在
一定在![]() 轴上,
轴上,
从而点![]() 的坐标为
的坐标为![]() 或
或![]() ,直线
,直线![]() 的方程为
的方程为![]() ,∴点
,∴点![]() 到直线
到直线![]() 的距离为1.
的距离为1.
∴点![]() 到直线
到直线![]() 的距离的最小值为
的距离的最小值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目