题目内容
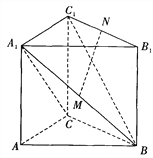
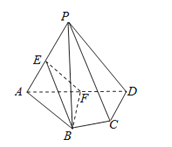
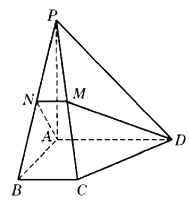
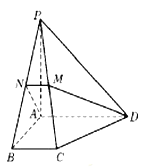
【题目】如图,在四棱锥![]() 中,底面为直角梯形,
中,底面为直角梯形, ![]() ,
, ![]() ,
, ![]() 垂直于底面
垂直于底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求四棱锥的体积![]() 和截面
和截面![]() 的面积.
的面积.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先根据线面垂直性质定理得![]() ,而
,而![]() ,所以由线面垂直判定定理得
,所以由线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() , 再由等腰三角形性质得
, 再由等腰三角形性质得![]() ,因此由线面垂直判定定理得
,因此由线面垂直判定定理得![]() 平面
平面![]() ,即证得
,即证得![]() ;(2)易得四棱锥
;(2)易得四棱锥![]() 的高
的高![]() ,再根据锥体体积公式得四棱锥的体积
,再根据锥体体积公式得四棱锥的体积![]() ;要求截面
;要求截面![]() 的面积,先确定截面
的面积,先确定截面![]() 的形状:由三角形中位线性质得
的形状:由三角形中位线性质得![]() ,即得
,即得![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,即四边形
,即四边形![]() 是直角梯形,最后利用直角梯形面积公式求解面积.
是直角梯形,最后利用直角梯形面积公式求解面积.
试题解析:(Ⅰ)证明:∵![]() 是
是![]() 的中点,
的中点, ![]() ,∴
,∴![]() ,
,
由![]() 底面
底面![]() ,得
,得![]() ,
,
又![]() ,即
,即![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]()
∴![]() .
.
(Ⅱ)解:由![]() ,得底面直角梯形
,得底面直角梯形![]() 的面积
的面积![]() ,
,
由![]() 底面
底面![]() ,得四棱锥
,得四棱锥![]() 的高
的高![]() ,
,
所以四棱锥![]() 的体积
的体积![]() .
.
由![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,得
的中点,得![]() ,且
,且![]() ,
,
又![]() ,故
,故![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
故![]() ,∴四边形
,∴四边形![]() 是直角梯形,
是直角梯形,
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴截面![]() 的面积
的面积![]() .
.

练习册系列答案
相关题目
【题目】一鲜花店根据一个月(30天)某种鲜花的日销售量与销售天数统计如下,将日销售量落入各组区间频率视为概率.
日销售量(枝) |
|
|
|
|
|
销售天数 | 3天 | 5天 | 13天 | 6天 | 3天 |
(1)试求这30天中日销售量低于100枝的概率;
(2)若此花店在日销售量低于100枝的时候选择2天作促销活动,求这2天恰好是在日销售量低于50枝时的概率.