Question

【题目】当n∈N*时， ，Tn= + + +…+ ． （Ⅰ）求S1 ， S2 ， T1 ， T2；
（Ⅱ）猜想Sn与Tn的关系，并用数学归纳法证明．

Answer 1

【答案】解：（Ⅰ）∵当n∈N*时， ，Tn= + + +…+ ． ∴S1=1﹣ = ，S2=1﹣ + ﹣ = ，T1= = ，T2= + =
（Ⅱ）猜想：Sn=Tn（n∈N*），即：
1﹣ + ﹣ +…+ ﹣ = + + +…+
（n∈N*）
下面用数学归纳法证明：
①当n=1时，已证S1=T1
②假设n=k时，Sk=Tk（k≥1，k∈N*），
即：1﹣ + ﹣ +…+ ﹣ = +…+
则：Sk+1=Sk+ ﹣ =Tk+ ﹣
= +…+ + ﹣
= +…+ + +（ ﹣ ）
= + +…+ + =Tk+1 ，
由①，②可知，对任意n∈N* ， Sn=Tn都成立．
【解析】（Ⅰ）由已知直接利用n=1，2，求出S1 ， S2 ， T1 ， T2的值；（Ⅱ）利用（1）的结果，直接猜想Sn=Tn ， 然后利用数学归纳法证明，①验证n=1时猜想成立；②假设n=k时，Sk=Tk ， 通过假设证明n=k+1时猜想也成立即可．
【考点精析】通过灵活运用数列的前n项和和数学归纳法的定义，掌握数列{an}的前n项和sn与通项an的关系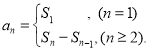；数学归纳法是证明关于正整数n的命题的一种方法即可以解答此题．