题目内容
为了保护环境,某工厂在国家的号召下,把废弃物回收转化为某种产品,经测算,处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: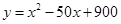 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为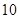 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴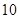 万元.
万元.
(1)当 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
如果不能获利,请求出国家最少补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?
(1)国家最少需要补贴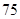 万元,该工厂才能不会亏损;(2)30.
万元,该工厂才能不会亏损;(2)30.
解析试题分析:(1)本题考查函数应用,属于容易题,解题的关键是列出收益函数,收益等于收入减成本,因此有利润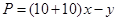 ,化简后它是关于
,化简后它是关于 的二次函数,利用二次函数的知识求出
的二次函数,利用二次函数的知识求出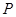 的取值范围,如果
的取值范围,如果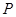 有非负的取值,就能说明可能获利,如果
有非负的取值,就能说明可能获利,如果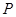 没有非负取值,说明不能获利,而国家最小补贴就是
没有非负取值,说明不能获利,而国家最小补贴就是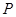 中最大值的绝对值.(2)每吨平均成本等于
中最大值的绝对值.(2)每吨平均成本等于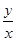 ,由题意
,由题意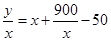 ,我们根据基本不等式的知识就可以求出它的最小值以及取最小值时的
,我们根据基本不等式的知识就可以求出它的最小值以及取最小值时的 值.
值.
试题解析:(1)根据题意得,利润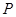 和处理量
和处理量 之间的关系:
之间的关系: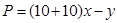
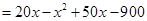
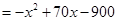 2分
2分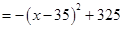 ,
,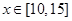 .
.
∵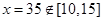 ,
,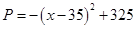 在
在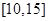 上为增函数,
上为增函数,
可求得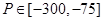 . 5分
. 5分
∴国家只需要补贴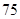 万元,该工厂就不会亏损. 7分
万元,该工厂就不会亏损. 7分
(2)设平均处理成本为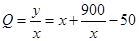 9分
9分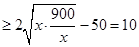 , 11分
, 11分
当且仅当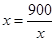 时等号成立,由
时等号成立,由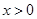 得
得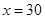 .
.
因此,当处理量为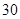 吨时,每吨的处理成本最少为
吨时,每吨的处理成本最少为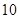 万元. 14分
万元. 14分
考点:函数应用题,二次函数的值域,基本不等式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若
,若 对于所有的
对于所有的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.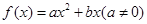 满足条件:①
满足条件:①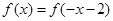 ;②函数
;②函数 的图像与直线
的图像与直线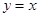 相切.
相切.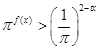 在
在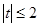 时恒成立,求实数
时恒成立,求实数 的取值范围.
的取值范围.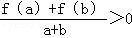 .
.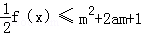 对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.
对所有x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数m的取值范围.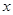 (单位:元,
(单位:元, )的平方成正比.
)的平方成正比.
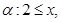 命题
命题 且命题
且命题 是
是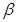 的必要条件,求实数m的取值范围
的必要条件,求实数m的取值范围 .
. 在
在 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围; 时,若对任意的
时,若对任意的 ,总存在
,总存在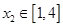 使
使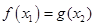 成立,求实数
成立,求实数 的取值范围.
的取值范围.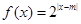 和函数
和函数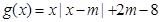 ,其中
,其中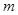 为参数,且满足
为参数,且满足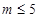 .
. ,写出函数
,写出函数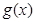 的单调区间(无需证明);
的单调区间(无需证明);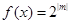 在
在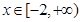 上有唯一解,求实数
上有唯一解,求实数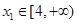 ,存在
,存在 ,使得
,使得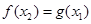 成立,求实数
成立,求实数