题目内容
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设![]() ,
,![]() ,
,![]() ,结合题意求得
,结合题意求得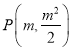 ,然后消去参数
,然后消去参数![]() 即可得解;
即可得解;
(2)结合题意,求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的坐标,然后结合三角形面积公式求解即可.
的坐标,然后结合三角形面积公式求解即可.
解:(1)设![]() ,
,![]() ,
,![]() ,
,
联立方程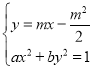 ,
,
得![]() ,
,
由![]() ,且
,且![]() ,
,
因此![]() ,
,
将其代入![]() 得
得![]() ,
,
因为![]() ,
,
所以![]() ,
,
∴![]() ,
,
所以直线![]() 方程为
方程为![]() ,
,
可得![]() ,
,
∴![]() ,
,
代入![]() ,得
,得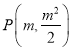 ,
,
消去![]() ,可得
,可得![]() 点的轨迹方程为
点的轨迹方程为![]() .
.
(2)根据题意,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
由(1)知,![]() ,
,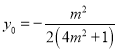 ,
,
对于直线![]() ,令
,令![]() ,
,![]() ,
,
所以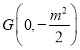 ,
,
所以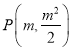 ,
,![]() ,
,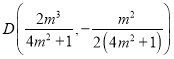 ,
,![]() ,
,
所以![]() ,
,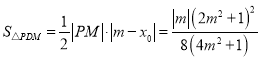 ,
,
所以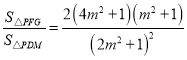 ,
,
令![]() ,
,
则![]() ,
,
当![]() ,
,
即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,
,
此时![]() ,满足
,满足![]() .
.
故![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
相关题目
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
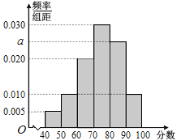
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |