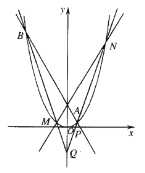
题目内容
【题目】定义:若向量列![]() ,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即
,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即![]() (
(![]() ,且
,且![]() ,
,![]() 为常向量),则称这个向量列
为常向量),则称这个向量列![]() 为等差向量列,这个常向量叫做等差向量列的公差,且向量列
为等差向量列,这个常向量叫做等差向量列的公差,且向量列![]() 的前
的前![]() 项和为
项和为![]() .已知等差向量列
.已知等差向量列![]() 满足
满足![]() ,则向量列
,则向量列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.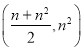 B.
B.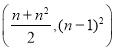
C.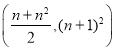 D.
D.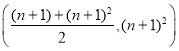
【答案】A
【解析】
根据题意分析等差数列的性质对于等差向量列也适合,再由等差数列的通项公式和前![]() 项和公式,可类比出等差向量列的通项公式和前
项和公式,可类比出等差向量列的通项公式和前![]() 项和公式,求解即可.
项和公式,求解即可.
由题易知等差数列的性质对于等差向量列也适合,类比等差数列的性质得![]() ,解得
,解得![]() ,所以等差向量列
,所以等差向量列![]() 的公差为
的公差为![]() .类比等差数列的通项公式,得等差向量列
.类比等差数列的通项公式,得等差向量列![]() 的通项公式为
的通项公式为![]()
![]() .进而再类比等差数列的前
.进而再类比等差数列的前![]() 项和公式,可以得到等差向量列
项和公式,可以得到等差向量列![]() 的前
的前![]() 项和公式为
项和公式为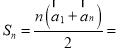
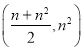 .
.
故选:A

练习册系列答案
相关题目