题目内容
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
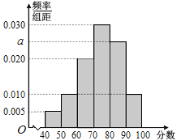
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
【答案】(1)![]() ,74.5分;(2)表格见解析,有
,74.5分;(2)表格见解析,有
【解析】
(1)根据频率和为1,求出![]() ,按照平均数公式,即可求解;
,按照平均数公式,即可求解;
(2)由频率直方图求出,在抽取的100名学生中,比赛成绩优秀的人数,补全列联表,求出![]() 的观测值,结合提供数据,即可得出结论.
的观测值,结合提供数据,即可得出结论.
(1)由题可得![]() ,
,
解得![]() .
.
因为![]()
![]() ,
,
所以估计这100名学生的平均成绩为74.5分
(2)由(1)知,在抽取的100名学生中,比赛成绩优秀的有![]() 人,由此可得完整的
人,由此可得完整的![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
∵![]() 的观测值
的观测值![]() ,
,
∴有![]() 的把握认为“比赛成绩是否优秀与性别有关”.
的把握认为“比赛成绩是否优秀与性别有关”.

【题目】为了进一步激发同学们的学习热情,某班级建立了数学英语两个学习兴趣小组,两组的人数如下表所示:
组别 性别 | 数学 | 英语 |
男 | 5 | 1 |
女 | 3 | 3 |
现采用分层抽样的方法(层内采用简单随机抽样)从两组中共抽取3名同学进行测试.
(1)求从数学组抽取的同学中至少有1名女同学的概率;
(2)记ξ为抽取的3名同学中男同学的人数,求随机变量ξ的分布列和数学期望.
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图(分组区间为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),并将分数从低到高分为四个等级:
),并将分数从低到高分为四个等级:
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
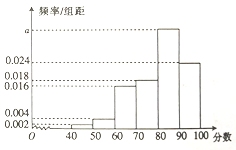
(1)求表中![]() 的值及不满意的人数;
的值及不满意的人数;
(2)在等级为不满意的师生中,老师占![]() ,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记
,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记![]() 为老师整改督导员的人数,求
为老师整改督导员的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某大型电器企业,为了解组装车间职工的生活情况,从中随机抽取了![]() 名职工进行测试,得到频数分布表如下:
名职工进行测试,得到频数分布表如下:
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
(1)现从参与测试的日组装个数少于![]() 的职工中任意选取
的职工中任意选取![]() 人,求至少有
人,求至少有![]() 人日组装个数少于
人日组装个数少于![]() 的概率;
的概率;
(2)由频数分布表可以认为,此次测试得到的日组装个数![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组数据用该组区间的中点值作为代表).
人得分的平均值(同一组数据用该组区间的中点值作为代表).
(![]() 名职工,求日组装个数超过
名职工,求日组装个数超过![]() 的职工人数;
的职工人数;
(ii)为鼓励职工提高技能,企业决定对日组装个数超过![]() 的职工日工资增加
的职工日工资增加![]() 元,若在组装车间所有职工中任意选取
元,若在组装车间所有职工中任意选取![]() 人,求这三人增加的日工资总额的期望.
人,求这三人增加的日工资总额的期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.