题目内容
【题目】给出下列四个命题:
①函数![]() 的最小值是2;
的最小值是2;
②等差数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() 取最大值;
取最大值;
③等比数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
④![]() ,
,![]() 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是![]() .
.
其中所有正确命题的序号是________________________.
【答案】②④
【解析】
①对式子变形并利用基本不等式,注意等号成立的条件不成立,从而可判断①错误;②由等差数列的前n项和公式以及下标和性质可得![]() ,
,![]() ,从而可判断②正确;③令
,从而可判断②正确;③令![]() ,可得到一个反例,从而判断③错误;④先考虑
,可得到一个反例,从而判断③错误;④先考虑![]() 时的情况,当
时的情况,当![]() 时,分离参数可得
时,分离参数可得![]() ,化简变形转化为求二次函数的最大值,从而可判断④正确.
,化简变形转化为求二次函数的最大值,从而可判断④正确.
①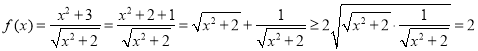 ,当且仅当
,当且仅当![]() 时,等号成立,此时
时,等号成立,此时![]() ,无解,故①错误;
,无解,故①错误;
②由![]() ,
,![]() ,
,
则![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 取最大值,故②正确;
取最大值,故②正确;
③令![]() ,则
,则![]() ,
,![]() ,但是
,但是![]() ,故③错误;
,故③错误;
④当![]() 时,不等式成立,
时,不等式成立,
当![]() 时,分离参数可得
时,分离参数可得![]() ,
,
则![]() ,又
,又![]() ,
,
所以![]() ,故④正确.
,故④正确.
所以本题答案为②④.

练习册系列答案
相关题目
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
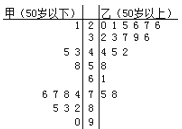
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |