题目内容
下列函数中既是奇函数，又在区间（0，1）内单调递减的函数是（ ）A．f（x）=sin
B．f（x）=-x|x|
C．f（x）=x3
D．
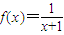
【答案】分析：A：f（x）=sinx，且在（0，1）上单调递增
B：f（x）是奇函数，当0＜x＜1时，f（x）=-x2在（0，1）上单调递减，
C：f（x）=x3在（0，1）上单调递增
D：f（x）=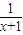
为非奇非偶函数
解答：解：f（x）=sinx是奇函数，且在（0，1）上单调递增，故A不符合题意
B：由f（x）=-x|x|可得，f（-x）=-（-x）x|-x|=x|x|=-f（x），是奇函数，且当0＜x＜1时，f（x）=-x2在（0，1）上单调递减，故B符合题意
C：f（x）=x3是奇函数且在（0，1）上单调递增，故C不符合题意
D：f（x）=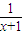
为非奇非偶函数，故D不符合题意
故选B
点评：本题主要考查了常见的基本初等函数的奇偶性及单调性的判断，属于基础试题
B：f（x）是奇函数，当0＜x＜1时，f（x）=-x2在（0，1）上单调递减，
C：f（x）=x3在（0，1）上单调递增
D：f（x）=
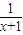为非奇非偶函数解答：解：f（x）=sinx是奇函数，且在（0，1）上单调递增，故A不符合题意
B：由f（x）=-x|x|可得，f（-x）=-（-x）x|-x|=x|x|=-f（x），是奇函数，且当0＜x＜1时，f（x）=-x2在（0，1）上单调递减，故B符合题意
C：f（x）=x3是奇函数且在（0，1）上单调递增，故C不符合题意
D：f（x）=
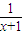为非奇非偶函数，故D不符合题意故选B
点评：本题主要考查了常见的基本初等函数的奇偶性及单调性的判断，属于基础试题
练习册系列答案
相关题目
已知函数f(x)=
，那么下列函数中既是奇函数又是周期函数的是（ ）
|
| A、y=f（x）sinx |
| B、y=f（x）+sinx |
| C、y=sin[f（x）] |
| D、y=f（sinx） |