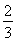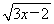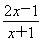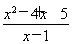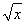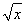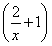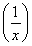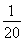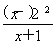Question

在平面直角坐标系xOy中，设定点A(a，a)，P是函数y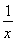＝(x>0)图象上一动点．若点P、A之间的最短距离为2 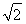，则满足条件的实数a的所有值为________．

 

Answer 1

－1，

【解析】设P 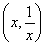，x>0，则

PA2＝(x－a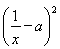)2＋＝x2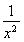＋－2a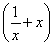＋2a2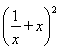＝－2a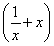＋2a2－2.

令t＝x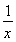＋，则由x>0，得t≥2，

所以PA2＝t2－2at＋2a2－2＝(t－a)2＋a2－2.

由PA取得最小值，得 或

解得a＝－1或a＝.