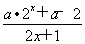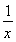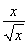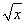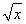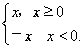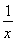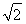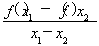题目内容
设函数f(x)= 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个不相同的实数根,求a取值的集合.
(1)f(x)= (2)
(2)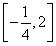
【解析】(1)∵当且仅当x=-2时,函数f(x)取得最小值-2.
∴二次函数y=x2+bx+c的对称轴是x=-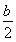 =-2.
=-2.
且有f(-2)=(-2)2-2b+c=-2,即2b-c=6.
∴b=4,c=2.∴f(x)=
(2)记方程①:2=x+a(x>0),
方程②:x2+4x+2=x+a(x≤0).
分别研究方程①和方程②的根的情况:
(ⅰ)方程①有且仅有一个实数根?a<2,方程①没有实数根?a≥2.
(ⅱ)方程②有且仅有两个不相同的实数根,即方程x2+3x+2-a=0有两个不相同的非正实数根.∴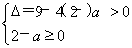 ?
? ?-
?-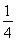 <a≤2;
<a≤2;
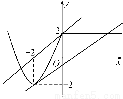
方程②有且仅有一个实数根,即方程x2+3x+2-a=0有且仅有一个非正实数根.
∴2-a<0或Δ=0,即a>2或a=-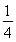 .
.
综上可知,当方程f(x)=x+a(a∈R)有三个不相同的实数根时,-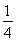 <a<2;
<a<2;
当方程f(x)=x+a(a∈R)有且仅有两个不相同的实数根时,a=-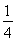 或a=2.
或a=2.
∴符合题意的实数a取值的集合为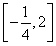

练习册系列答案
相关题目