题目内容
已知a、b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则f(x)在[-1,0]上的最小值为________.
-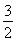
【解析】因为a、b为正实数,所以函数f(x)是单调递增的.所以f(1)=a+b+2=4,即a+b=2.所以f(x)在[-1,0]上的最小值为f(-1)=-(a+b)+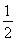 =-
=-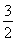 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知a、b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则f(x)在[-1,0]上的最小值为________.
-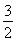
【解析】因为a、b为正实数,所以函数f(x)是单调递增的.所以f(1)=a+b+2=4,即a+b=2.所以f(x)在[-1,0]上的最小值为f(-1)=-(a+b)+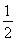 =-
=-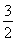 .
.

 阅读快车系列答案
阅读快车系列答案