题目内容
4.已知椭圆上一点与两个焦点的距离之和为10,焦距是函数:f(x)=x2-6x-16的零点.则椭圆的标准方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$或$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{9}=1$.分析 由题意,f(x)=x2-6x-16的零点为-2,8,焦距是函数:f(x)=x2-6x-16的零点,可得c=4,利用椭圆上一点与两个焦点的距离之和为10,可得a=5,b=3,即可写出椭圆的标准方程.
解答 解:由题意,f(x)=x2-6x-16的零点为-2,8,焦距是函数:f(x)=x2-6x-16的零点,∴2c=8,c=4
∵椭圆上一点与两个焦点的距离之和为10,
∴2a=10,∴a=5,
∴b=3,
∴椭圆的标准方程为$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$或$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{9}=1$.
故答案为:$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1$或$\frac{{y}^{2}}{25}+\frac{{x}^{2}}{9}=1$.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
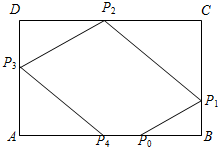 如图,矩形ABCD中,AB=3,AD=2,一质点从AB边上的点P0出发,沿与AB的夹角为θ的方向射到边BC上点P1后,依次反射(入射角与反射角相等)到边CD,DA和AB上的P2,P3,P4处.
如图,矩形ABCD中,AB=3,AD=2,一质点从AB边上的点P0出发,沿与AB的夹角为θ的方向射到边BC上点P1后,依次反射(入射角与反射角相等)到边CD,DA和AB上的P2,P3,P4处.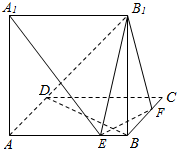 如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)
如图,正方形ABCD所在平面与正方形ABB1A1所在的平面垂直,且AB等于1.设E、F分别为AB、BC上的动点,(不包括端点)